The picture below shows the structures one finds by explicitly testing the first two billion possible initial conditions for the code 357 cellular automaton from page 282.
Already with initial condition number 28 a fairly complicated structure with repetition period 48 is seen. But with all the first million initial conditions, only one other structure is produced, and this structure is again one that does not move.
So are moving structures in fact possible in the code 357 cellular automaton? My experience with many different rules is that whenever sufficiently complicated persistent structures occur, structures that move can eventually be found. And indeed with code 357, initial condition 4,803,890 yields just such a structure.
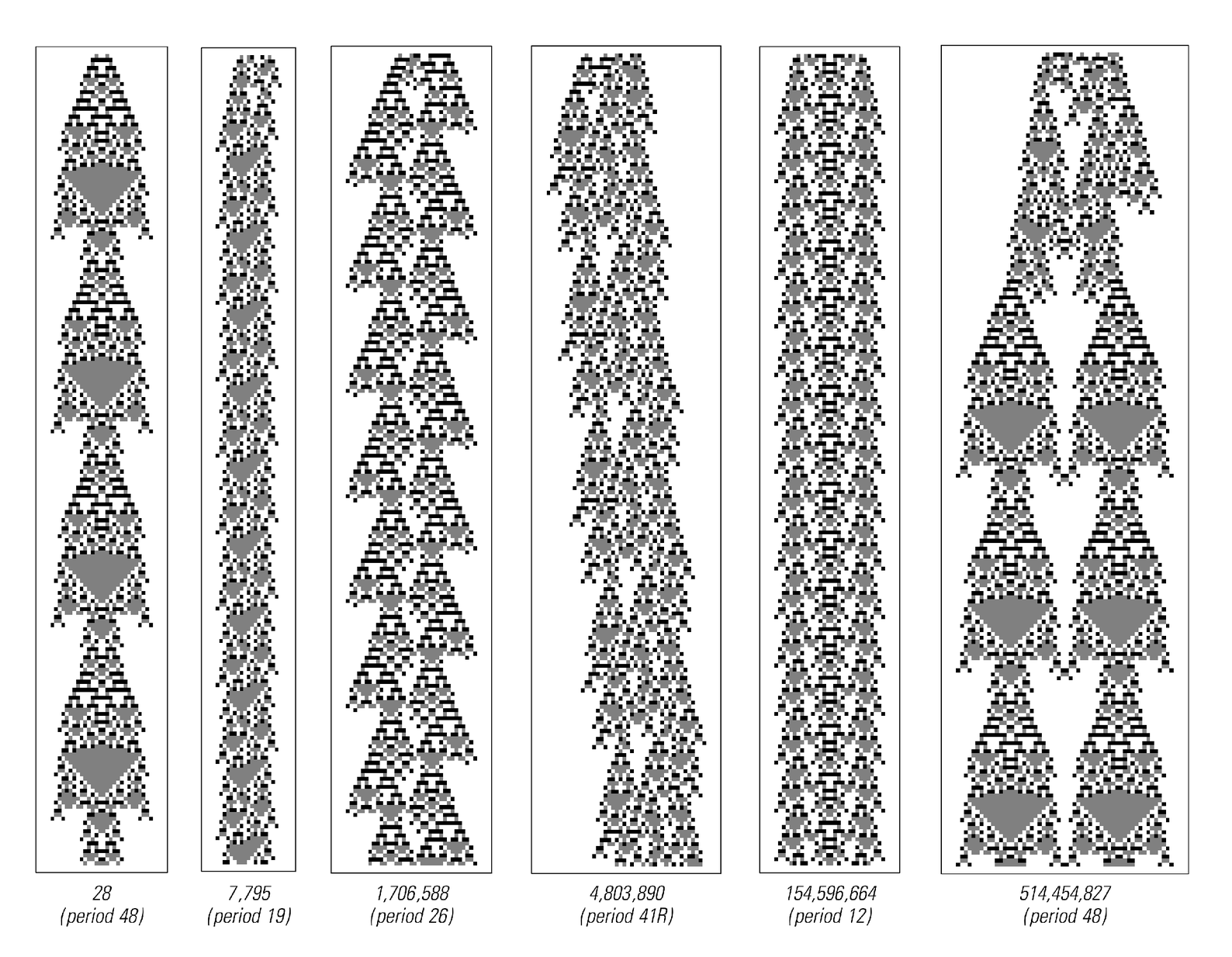
Persistent structures in the code 357 cellular automaton from page 282 obtained by testing the first two billion possible initial conditions. This cellular automaton allows three possible colors for each cell; the initial conditions thus correspond to the base 3 digits of the numbers given. No persistent structures of any size exist in this cellular automaton with repetition periods of less than 5 steps.



