doubled. And when the material is cut and stacked, the effect on the number is then to extract its fractional part.

But it turns out that this process is exactly the same as the one we discussed on page 153 in the chapter on systems based on numbers.

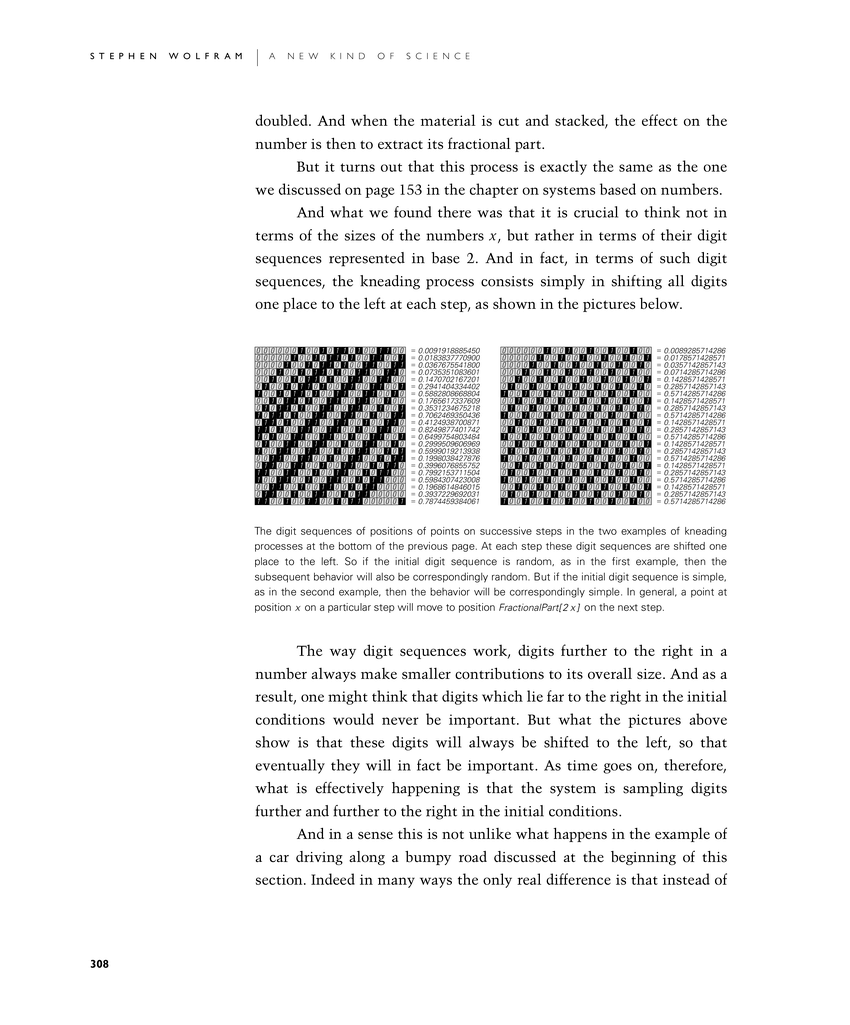
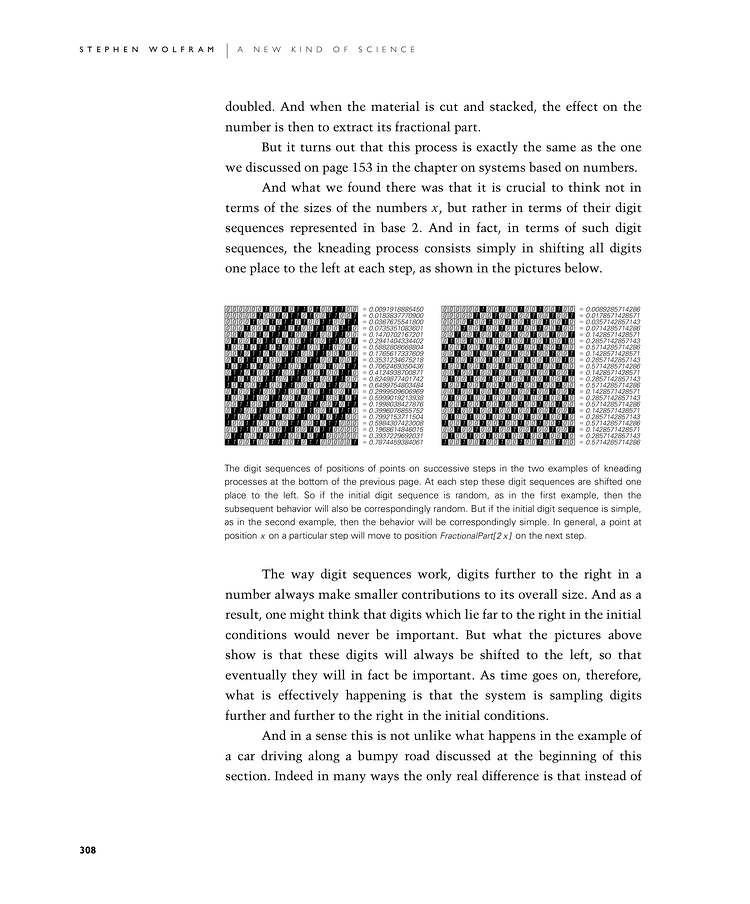
And what we found there was that it is crucial to think not in terms of the sizes of the numbers x, but rather in terms of their digit sequences represented in base 2. And in fact, in terms of such digit sequences, the kneading process consists simply in shifting all digits one place to the left at each step, as shown in the pictures below.

The way digit sequences work, digits further to the right in a number always make smaller contributions to its overall size. And as a result, one might think that digits which lie far to the right in the initial conditions would never be important. But what the pictures above show is that these digits will always be shifted to the left, so that eventually they will in fact be important. As time goes on, therefore, what is effectively happening is that the system is sampling digits further and further to the right in the initial conditions.

And in a sense this is not unlike what happens in the example of a car driving along a bumpy road discussed at the beginning of this section. Indeed in many ways the only real difference is that instead of

The digit sequences of positions of points on successive steps in the two examples of kneading processes at the bottom of the previous page. At each step these digit sequences are shifted one place to the left. So if the initial digit sequence is random, as in the first example, then the subsequent behavior will also be correspondingly random. But if the initial digit sequence is simple, as in the second example, then the behavior will be correspondingly simple. In general, a point at position x on a particular step will move to position FractionalPart[2x] on the next step.