A typical kind of failure, illustrated in the pictures on the next page, is that points with coordinates determined by successive numbers from the generator turn out to be distributed in an embarrassingly regular way. At first, such failures might suggest that more complicated schemes must be needed if one is to get good randomness. And indeed with this thought in mind all sorts of elaborate combinations of linear congruential and other generators have been proposed. But although some aspects of the behavior of such systems can be made quite random, deviations from perfect randomness are still often found.
And seeing this one might conclude that it must be essentially impossible to produce good randomness with any kind of system that has reasonably simple rules. But the rule 30 cellular automaton that we discussed above demonstrates that in fact this is absolutely not the case.
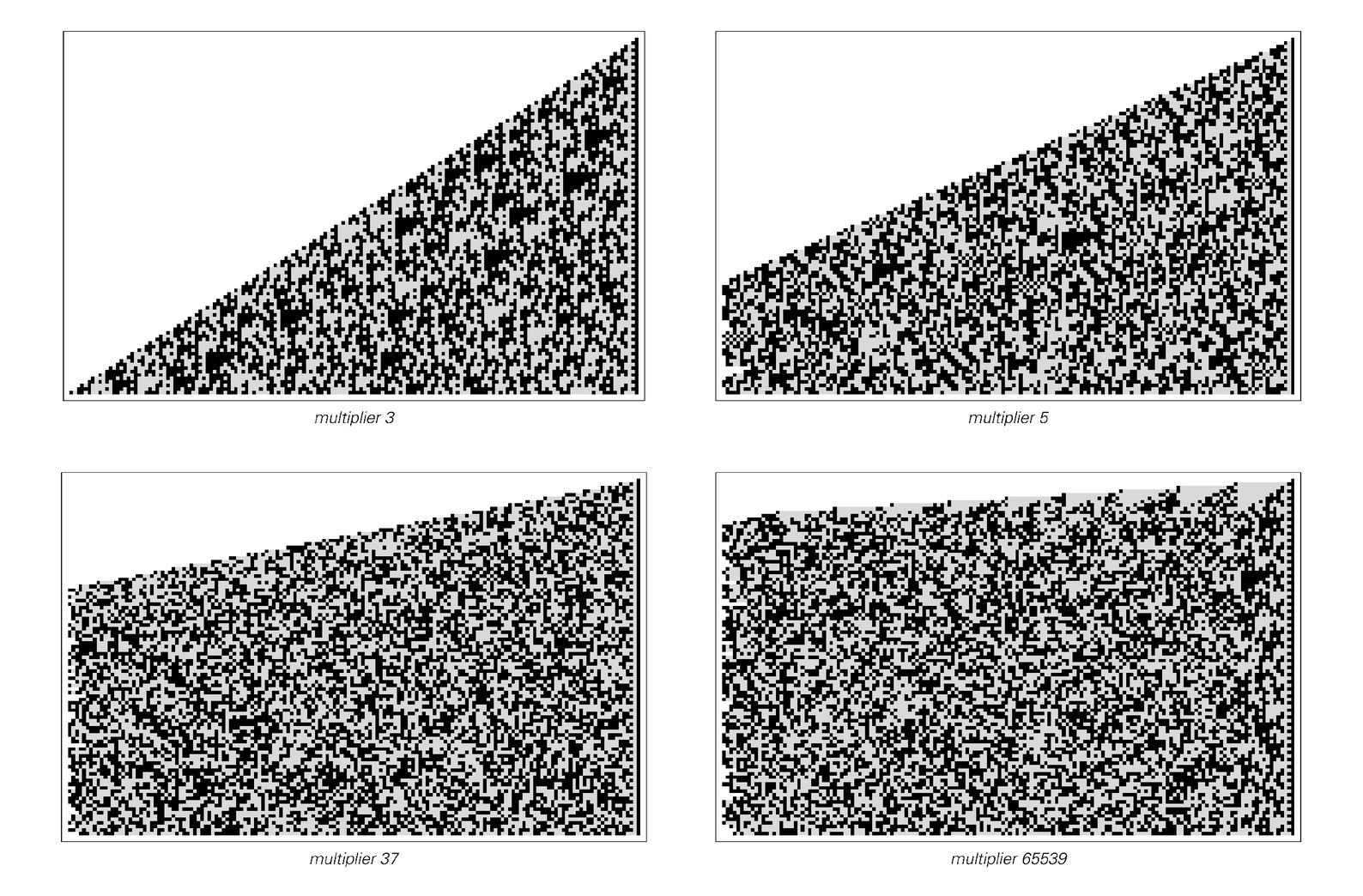
Patterns of digits in base 2 produced by starting with the number 1 and then repeatedly multiplying by various fixed constants. In all cases, the complete pattern has a triangular form, but except in the first case, it is truncated on the left here. The mathematical structure of these systems is nevertheless such that digits further to the left do not affect those shown: at each step the number obtained is effectively reduced modulo 2n, where n is the width of the picture.