In most cellular automata, the behavior obtained after a long time is either largely independent of the initial density, or varies quite smoothly with it. But the special feature of the cellular automata shown on the facing page is that they have two very different stable states—either all white or all black—and when one changes the initial density a discrete transition occurs between these two states.
One might think that the existence of such a discrete transition must somehow be associated with the discrete nature of the underlying cellular automaton rules. But it turns out that it is also possible to get such transitions in systems that have continuous underlying rules.
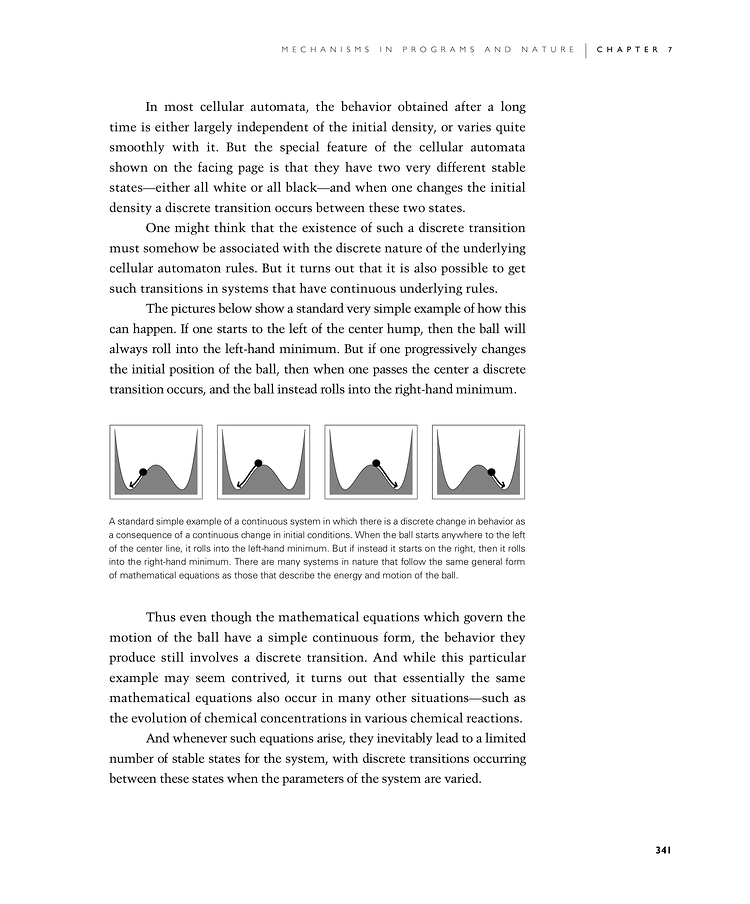
The pictures below show a standard very simple example of how this can happen. If one starts to the left of the center hump, then the ball will always roll into the left-hand minimum. But if one progressively changes the initial position of the ball, then when one passes the center a discrete transition occurs, and the ball instead rolls into the right-hand minimum.
Thus even though the mathematical equations which govern the motion of the ball have a simple continuous form, the behavior they produce still involves a discrete transition. And while this particular example may seem contrived, it turns out that essentially the same mathematical equations also occur in many other situations—such as the evolution of chemical concentrations in various chemical reactions.
And whenever such equations arise, they inevitably lead to a limited number of stable states for the system, with discrete transitions occurring between these states when the parameters of the system are varied.

A standard simple example of a continuous system in which there is a discrete change in behavior as a consequence of a continuous change in initial conditions. When the ball starts anywhere to the left of the center line, it rolls into the left-hand minimum. But if instead it starts on the right, then it rolls into the right-hand minimum. There are many systems in nature that follow the same general form of mathematical equations as those that describe the energy and motion of the ball.