below, is that some process can start at one point in space and then progressively spread, doing the same thing at every point it reaches.
Another mechanism is that every part of a system can evolve completely independently to the same state, as in the second set of pictures below.
A slightly less straightforward mechanism is illustrated in the third set of pictures below. Here different elements in the system do interact, but the result is still that all of them evolve to the same state.
So far all the mechanisms for uniformity I have mentioned involve behavior that is in a sense simple at every level. But in nature uniformity often seems to be associated with quite complex microscopic behavior. Most often what happens is that on a small scale a system exhibits randomness, but on a larger scale this randomness averages out to leave apparent uniformity, as in the fourth set of pictures below.
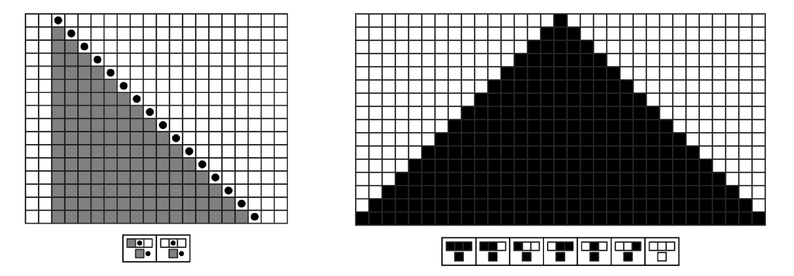
Homogenous growth from a single point is one straightforward way that uniformity in space can be produced, here illustrated in a mobile automaton and a cellular automaton.
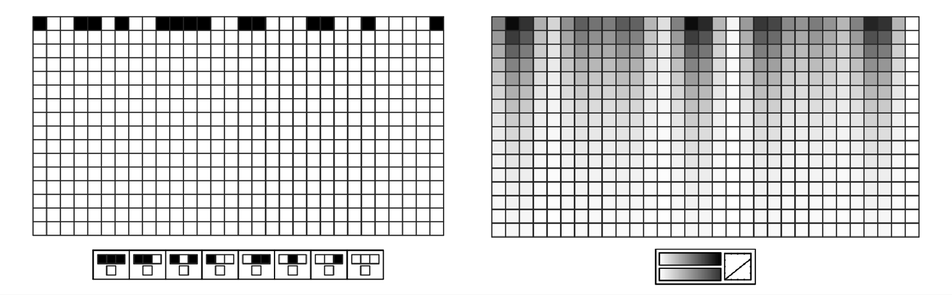
Uniformity in space can be achieved almost trivially if each element in a system independently evolves to the same state.
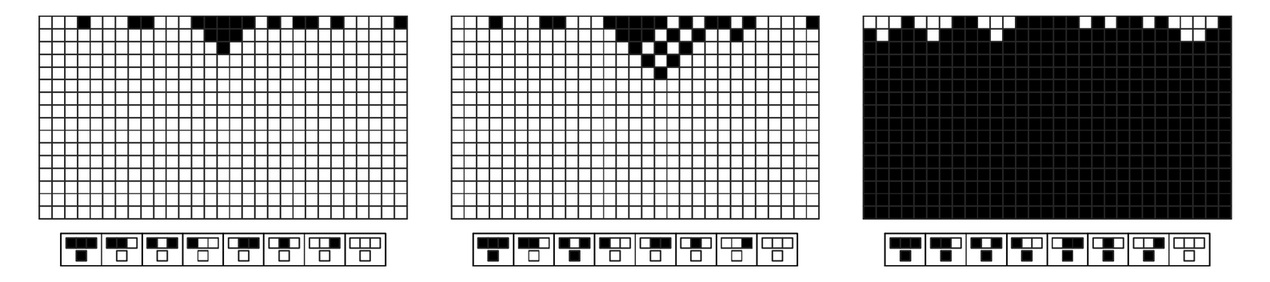
Class 1 cellular automata that exhibit evolution to a uniform state, as discussed in Chapter 6.

Averaging out small-scale randomness yields apparent uniformity, as shown here for a rule 30 pattern.