A somewhat related source of nesting relevant in many mathematical systems is the nested pattern formed by the digit sequences of successive numbers, as illustrated on page 117.
But in general nesting need not just arise from larger elements being broken down into smaller ones: for as we have discovered in this book it can also arise when larger elements are built up from smaller ones—and indeed I suspect that this is its more common origin in nature.
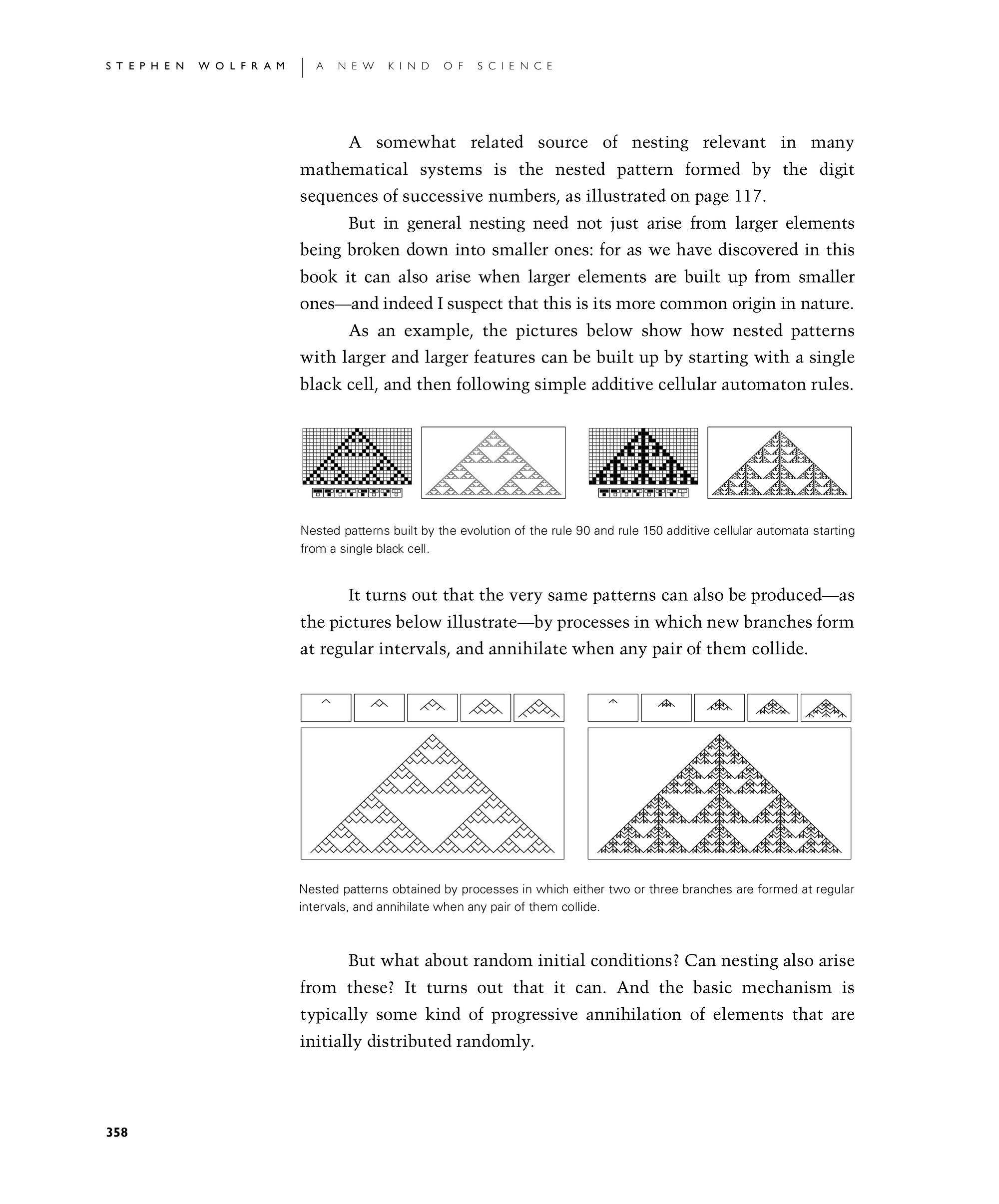
As an example, the first set of pictures below show how nested patterns with larger and larger features can be built up by starting with a single black cell, and then following simple additive cellular automaton rules.
It turns out that the very same patterns can also be produced—as the second set of pictures below illustrate—by processes in which new branches form at regular intervals, and annihilate when any pair of them collide.
But what about random initial conditions? Can nesting also arise from these? It turns out that it can. And the basic mechanism is typically some kind of progressive annihilation of elements that are initially distributed randomly.

Nested patterns built by the evolution of the rule 90 and rule 150 additive cellular automata starting from a single black cell.
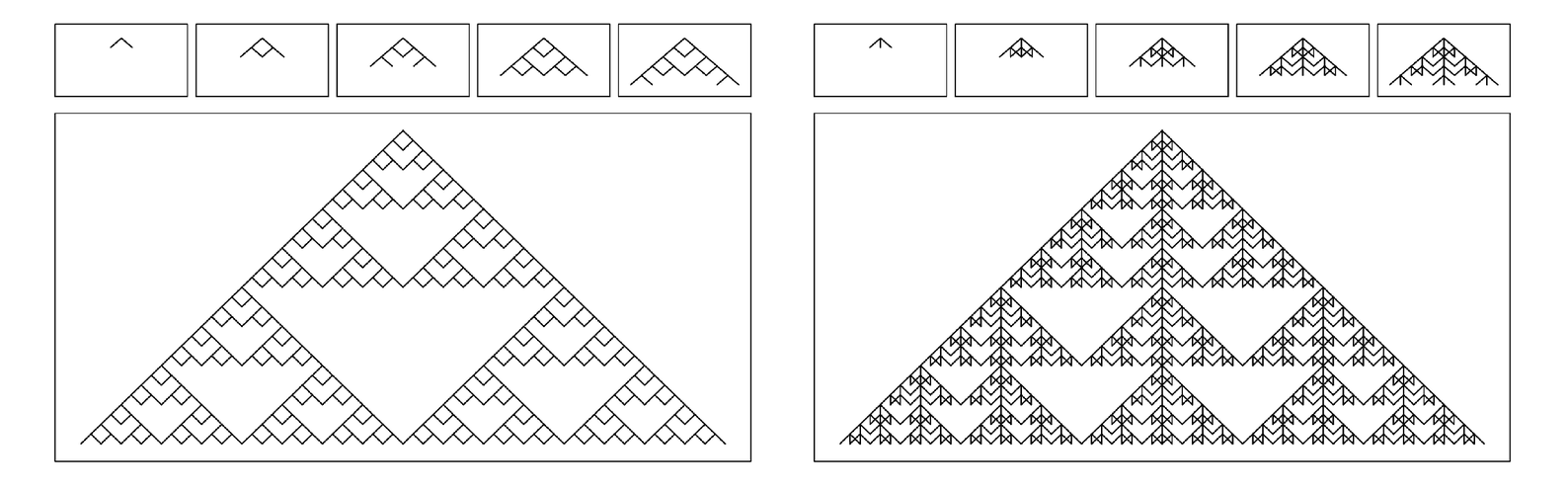
Nested patterns obtained by processes in which either two or three branches are formed at regular intervals, and annihilate when any pair of them collide.