simple models do not necessarily have simple behavior. And indeed the picture below shows an example of the behavior that can occur.
In real markets, it is usually impossible to see in detail what each entity is doing. Indeed, often all that one knows is the sequence of prices at which trades are executed. And in a simple cellular automaton the rough analog of this is the running difference of the total numbers of black and white cells obtained on successive steps.
And as soon as the underlying rule for the cellular automaton is such that information will eventually propagate from one entity to all others—in effect a minimal version of an efficient market hypothesis—it is essentially inevitable that running totals of numbers of cells will exhibit significant randomness.
One can always make the underlying system more complicated—say by having a network of cells, or by allowing different cells to have different and perhaps changing rules. But although this will make it more difficult to recognize definite rules even if one looks at the complete behavior of every element in the system, it does not affect the basic point that there is randomness that can intrinsically be generated by the evolution of the system.
 | 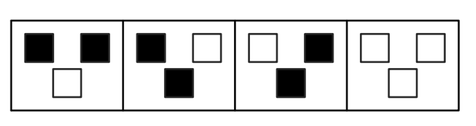 | 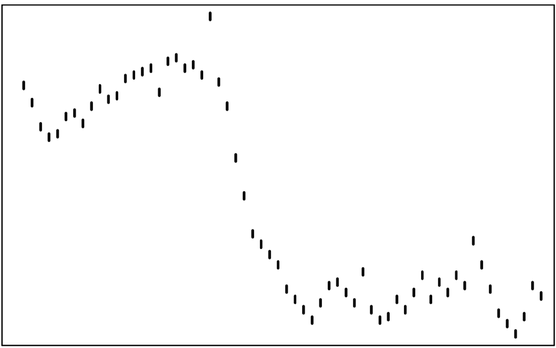 |
An example of a very simple idealized model of a market. Each cell corresponds to an entity that either buys or sells on each step. The behavior of a given cell is determined by looking at the behavior of its two neighbors on the step before according to the rule shown. The bottom-right plot below gives as a rough analog of a market price the running difference of the total numbers of black and white cells at successive steps. And although there are patches of predictability that can be seen in the complete behavior of the system the bottom-right plot looks in many respects random.



