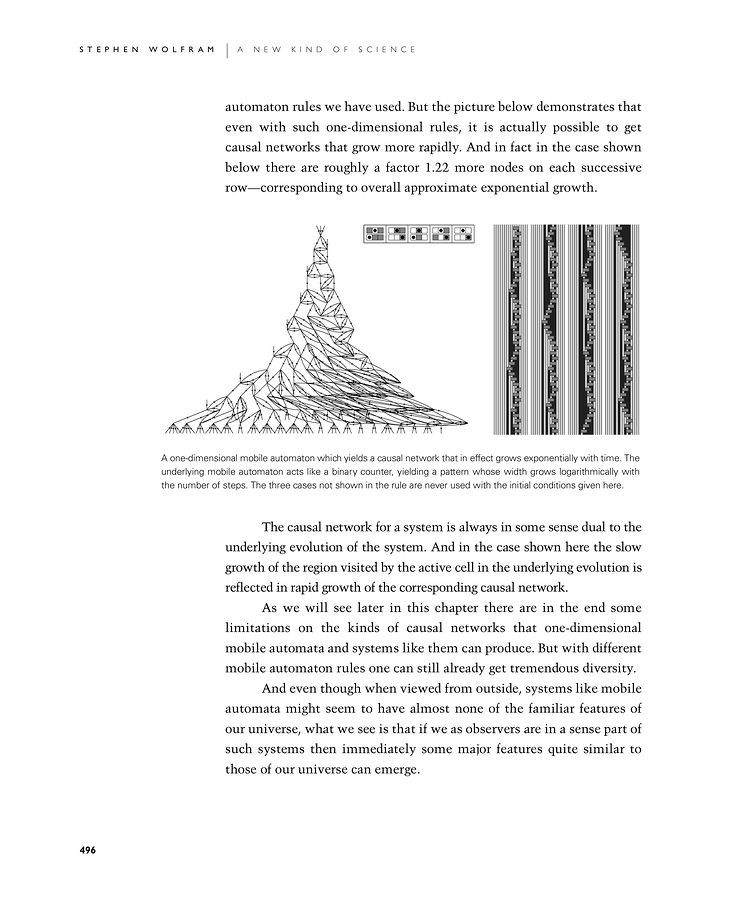
automaton rules we have used. But the picture below demonstrates that even with such one-dimensional rules, it is actually possible to get causal networks that grow more rapidly. And in fact in the case shown below there are roughly a factor 1.22 more nodes on each successive row—corresponding to overall approximate exponential growth.

The causal network for a system is always in some sense dual to the underlying evolution of the system. And in the case shown here the slow growth of the region visited by the active cell in the underlying evolution is reflected in rapid growth of the corresponding causal network.

As we will see later in this chapter there are in the end some limitations on the kinds of causal networks that one-dimensional mobile automata and systems like them can produce. But with different mobile automaton rules one can still already get tremendous diversity.

And even though when viewed from outside, systems like mobile automata might seem to have almost none of the familiar features of our universe, what we see is that if we as observers are in a sense part of such systems then immediately some major features quite similar to those of our universe can emerge.

A one-dimensional mobile automaton which yields a causal network that in effect grows exponentially with time. The underlying mobile automaton acts like a binary counter, yielding a pattern whose width grows logarithmically with the number of steps. The three cases not shown in the rule are never used with the initial conditions given here.