 |  |
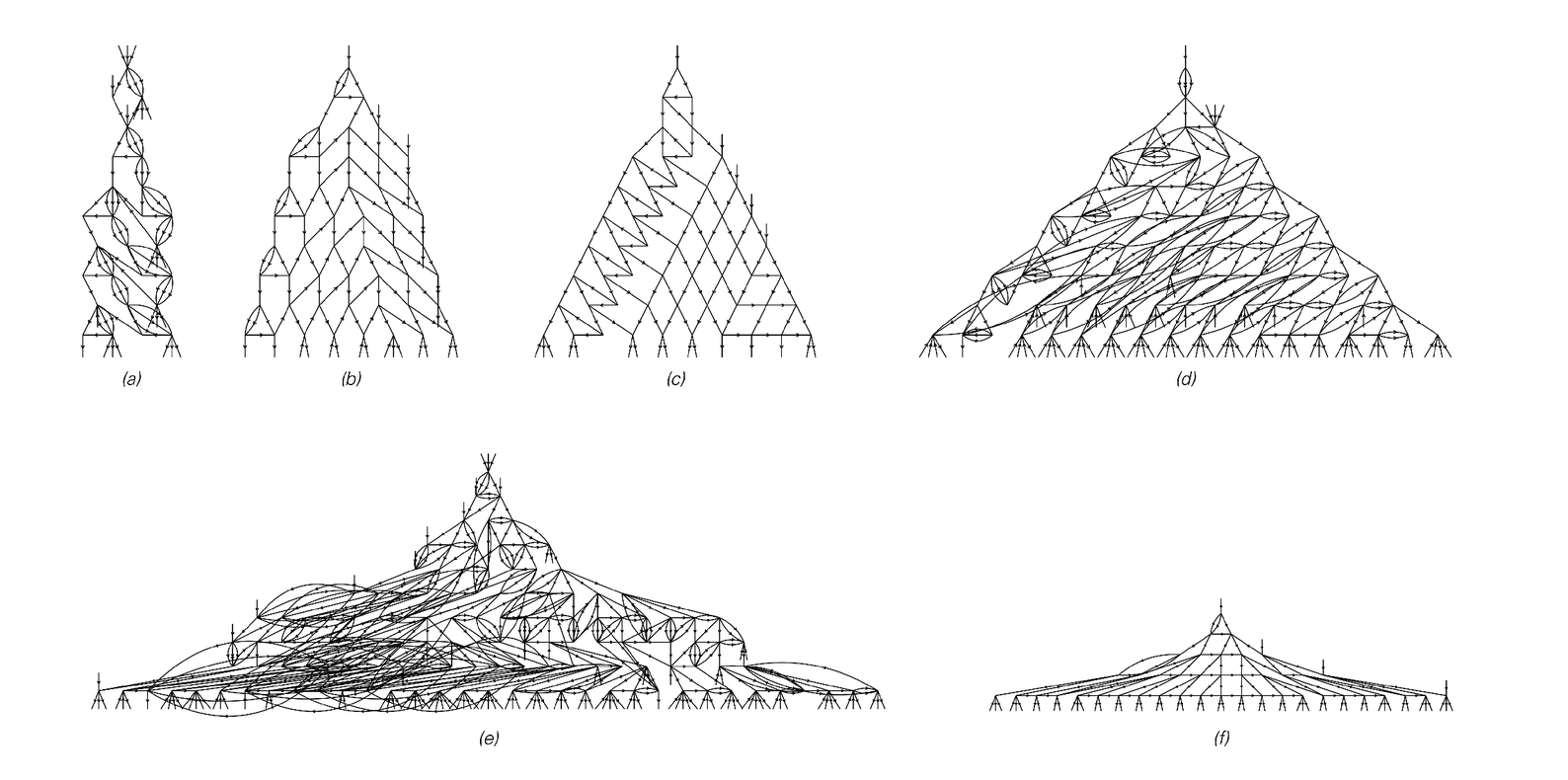
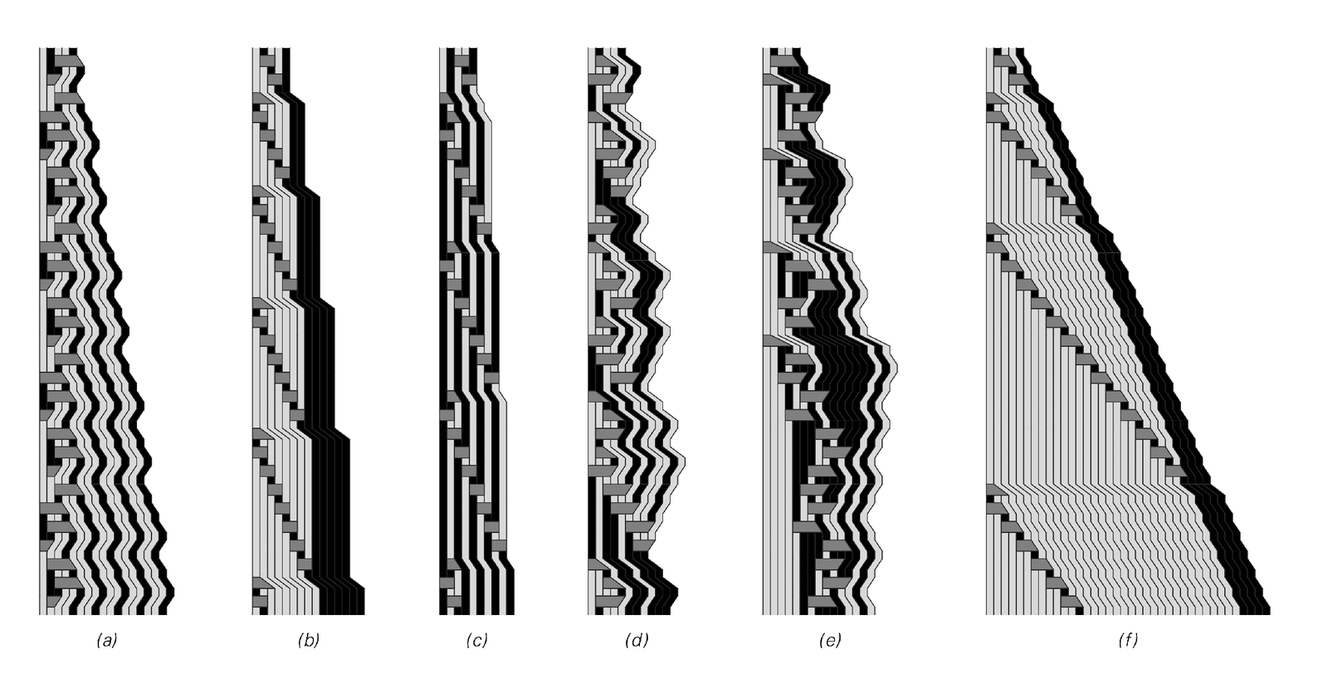
Examples of sequential substitution systems of the type discussed on page 88, and the causal networks that emerge from them. In a sequential substitution system only the first replacement that is found to apply in a left-to-right scan is ever performed at any step. Rule (a) above yields a causal network that is purely repetitive and thus yields no meaningful notion of space. Rules (b), (c) and (d) yield causal networks that in effect grow roughly linearly with time. In rule (f) the causal network grows exponentially, while in rule (e) the causal network also grows quite rapidly, though its overall growth properties are not clear. Note that to obtain the 10 levels shown here in the causal network for rule (e), it was necessary to follow the evolution of the underlying substitution system for a total of 258 steps.



