Uniqueness and Branching in Time
If our universe has no built-in global clock and no construct like an active cell, then it is almost inevitable that at the lowest level there will be at least some arbitrariness in how its rules can be applied.
Yet in the previous section we discovered the rather remarkable fact that there exist rules with the property that essentially regardless of how they are applied, the same causal network—and thus the same perceived history for the universe—will always emerge.
But must it in the end actually be true that the underlying rules for our universe force there to be a unique perceived history? Near the end of Chapter 5 I introduced multiway systems as examples of systems that allow multiple histories. And it turns out that multiway systems are actually extremely similar in basic structure to the substitution systems that I discussed in the previous section.
Both types of systems perform the same type of replacements on strings of elements. But while in a substitution system one always carries out just a single set of replacements at each step, getting a single new string, in a multiway system one instead carries out every possible replacement, thereby typically generating many new strings.
The picture below shows a simple example of how this works. On the first step in this particular picture, there happens to be only one replacement that can be performed consistent with the rules, so only a single string is produced. But on subsequent steps several different replacements are possible, so several strings are produced. And in general every path through a picture like this corresponds to a possible history that exists in the evolution of the multiway system.
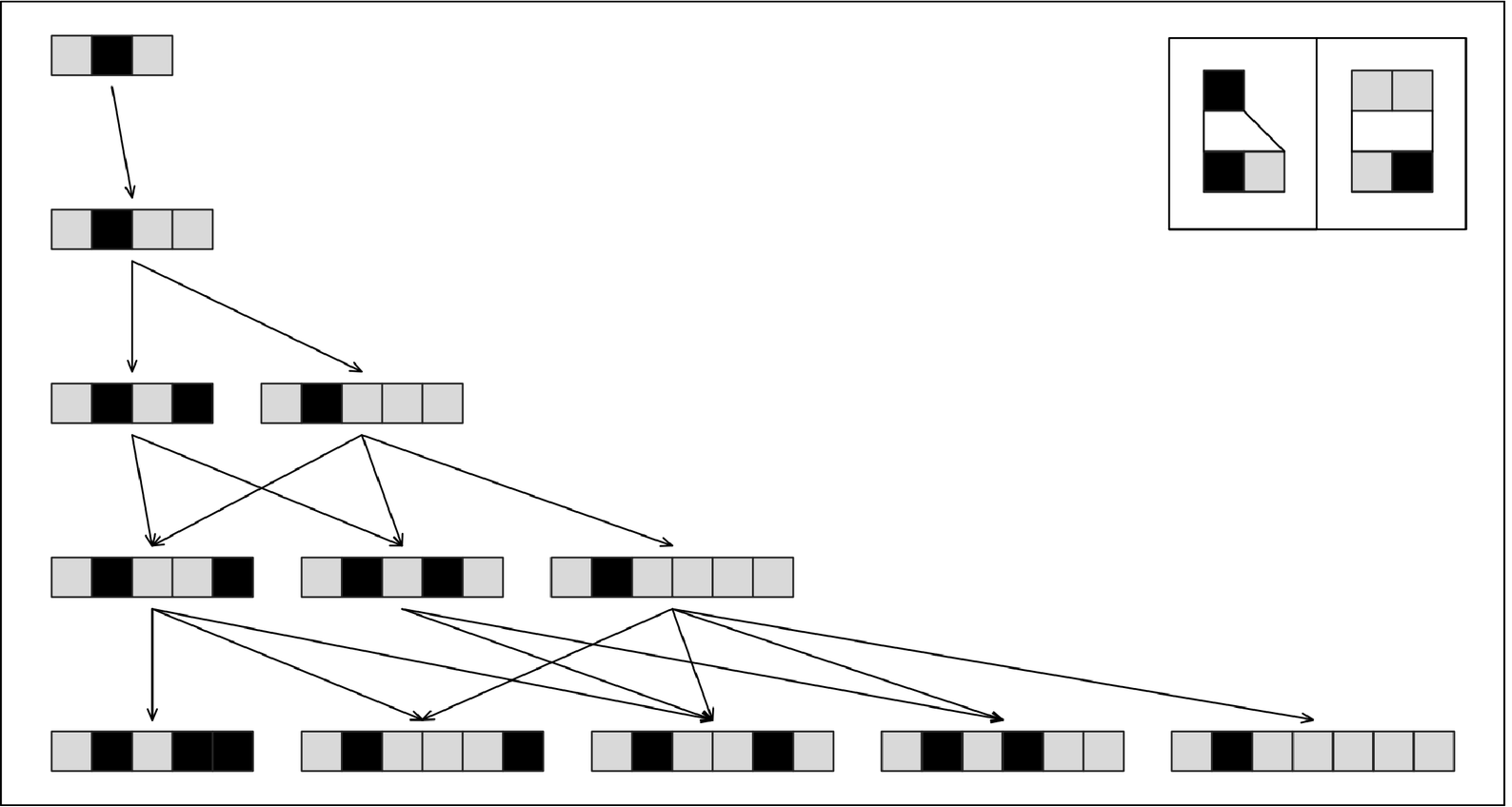
A simple example of a multiway system in which replacements are applied in all possible ways to each string at each step.