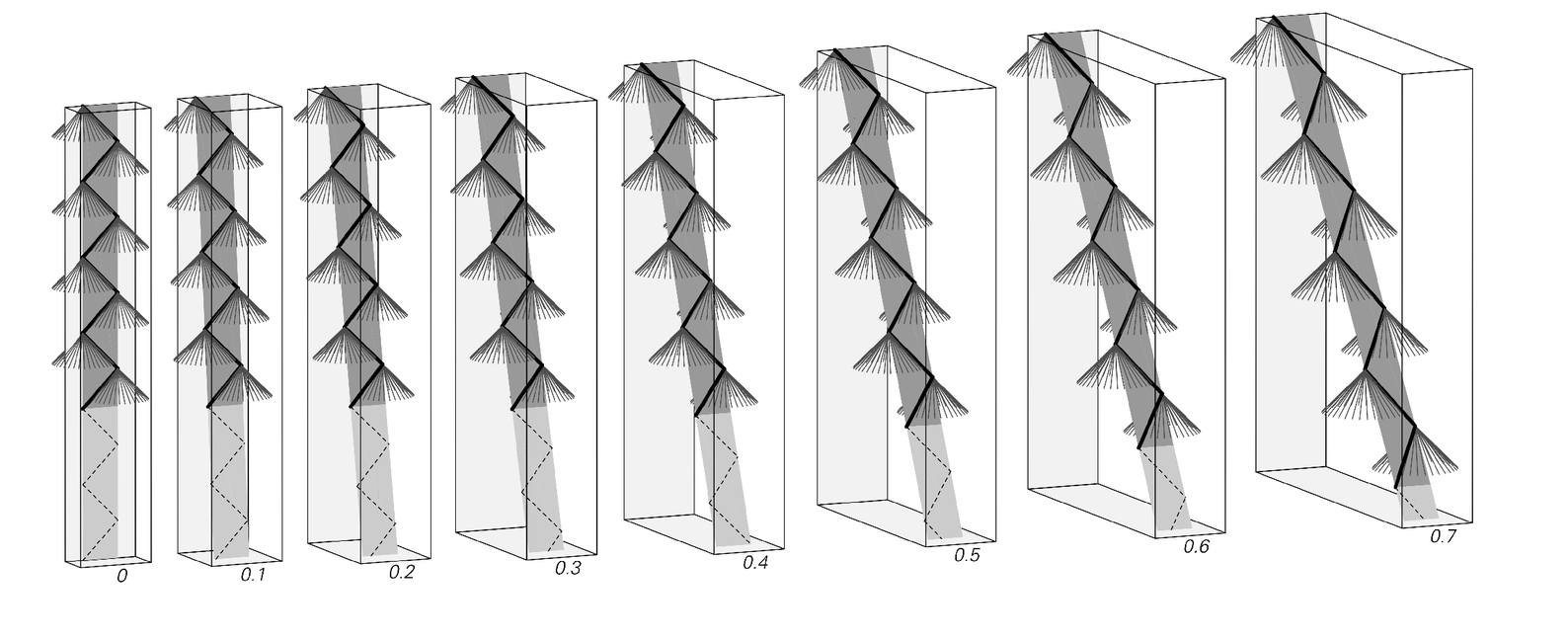
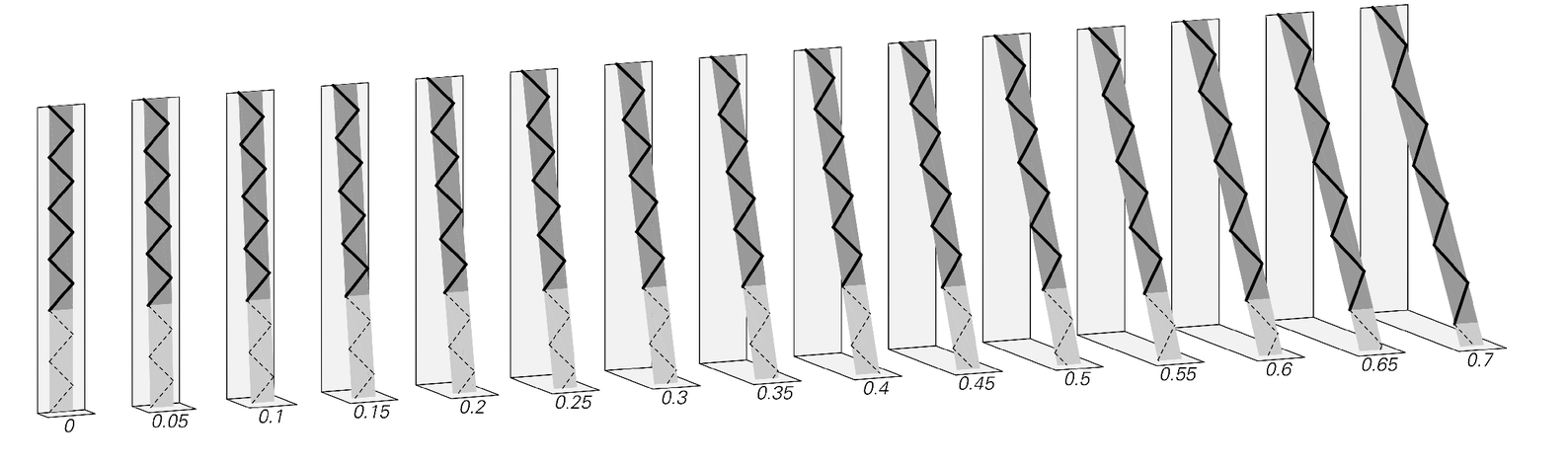
A simple derivation of the classic phenomenon of relativistic time dilation. The pictures show the behavior of a very simple idealized clock going at different fractions of the speed of light. The clock can be thought of as consisting of a photon of light bouncing backwards and forwards between mirrors a fixed distance apart. (At a more general level in my approach it can also be thought of as a fragment of a causal network.) Time is shown going down the page, so that the photon in the clock traces out a zig-zag path. The fundamental assumption—that in my approach is just a consequence of basic properties of causal networks—is that the photon always goes at the speed of light, so that its path always lies on the surface of light cones like the ones in the top row of pictures. A fixed interval of time for the clock—as indicated by the length of the darker gray regions—corresponds to a progressively longer interval of time at rest. The amount of this time dilation is given by the classic relativistic formula 1/Sqrt[1-v2/c2], where v/c is the ratio of the speed of the clock to the speed of light. Such time dilation is routinely observed in particle accelerators—and has to be corrected for in GPS satellites. It leads to the so-called twin paradox in which less time will pass for a member of a twin going at high speed in a spacecraft than one staying at rest. The fact that time dilation is a general phenomenon not restricted to something like the simple clock shown relies in my approach on general properties of causal networks. Once the basic assumptions are established, the derivation of time dilation given here is no different in principle from the original one given in 1905, though I believe it is in many ways considerably clearer. Note that it is necessary to consider motion in two dimensions—so that the clock as a whole can be moving perpendicular to the path of the photon inside it. If these were parallel, one would inevitably get not just pure time dilation, but a mixture of it and length contraction.



