has the property that its vertical position ends with a 0, and its horizontal position ends with a 1. So if the numbers that correspond to the position of a particular square contain this combination of digits at any point, it follows that the square must be white.
So what about other nested patterns? It turns out that using an extension of the argument above it is always possible to take the rules
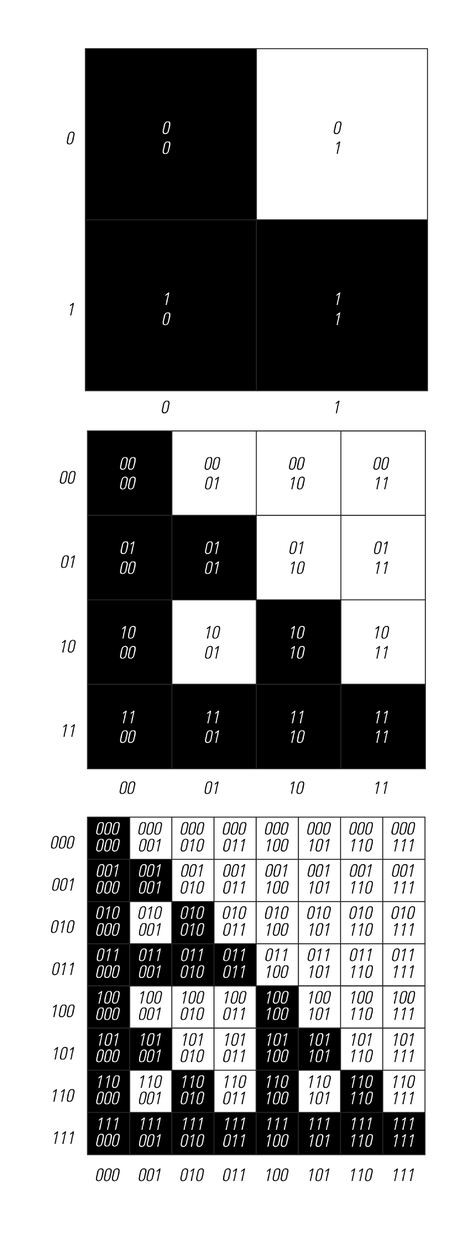 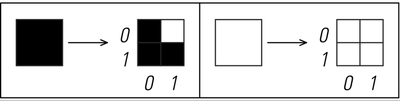 |  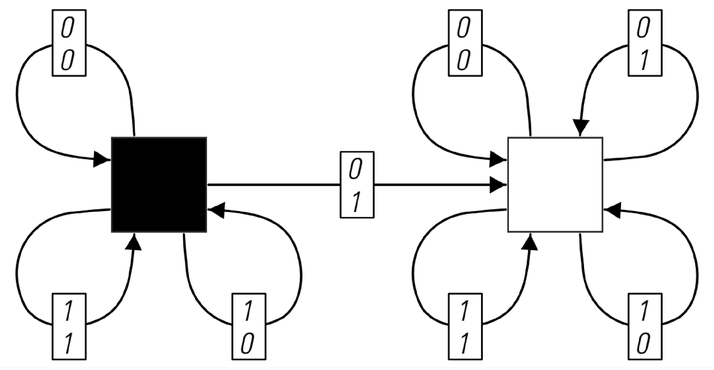 |
An example of how the color of any square in a nested pattern can be found from its coordinates by a fairly simple mathematical procedure. The procedure works by looking at the base 2 digit sequences of the coordinates. If any digit in the y coordinate of a particular square is 0 when the corresponding digit in the x coordinate is 1 then the square is white; otherwise it is black. The finite automaton at the bottom right gives a representation of this rule. Starting from the black square, one follows the sequence of connections that corresponds to the successive digits that one encounters in the y and x coordinates. Whatever square one lands up at in the finite automaton then gives the color one wants. Why this procedure works is illustrated by the pictures on the left. The nested pattern can be built up by a 2D substitution system with the rules shown. At each step in the evolution of this substitution system one gets a finer grid of squares, each specified in effect by one more digit in their coordinates.



