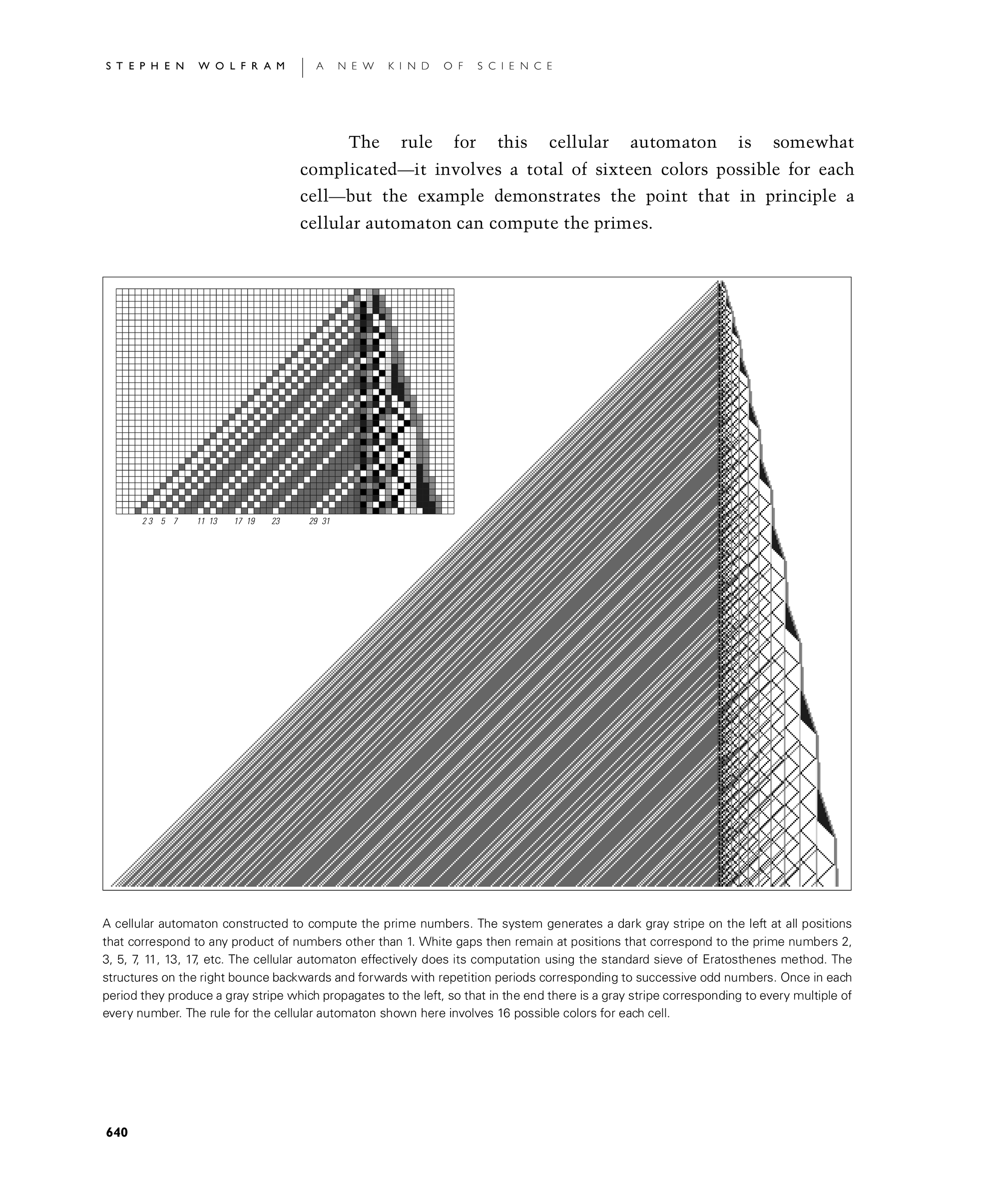
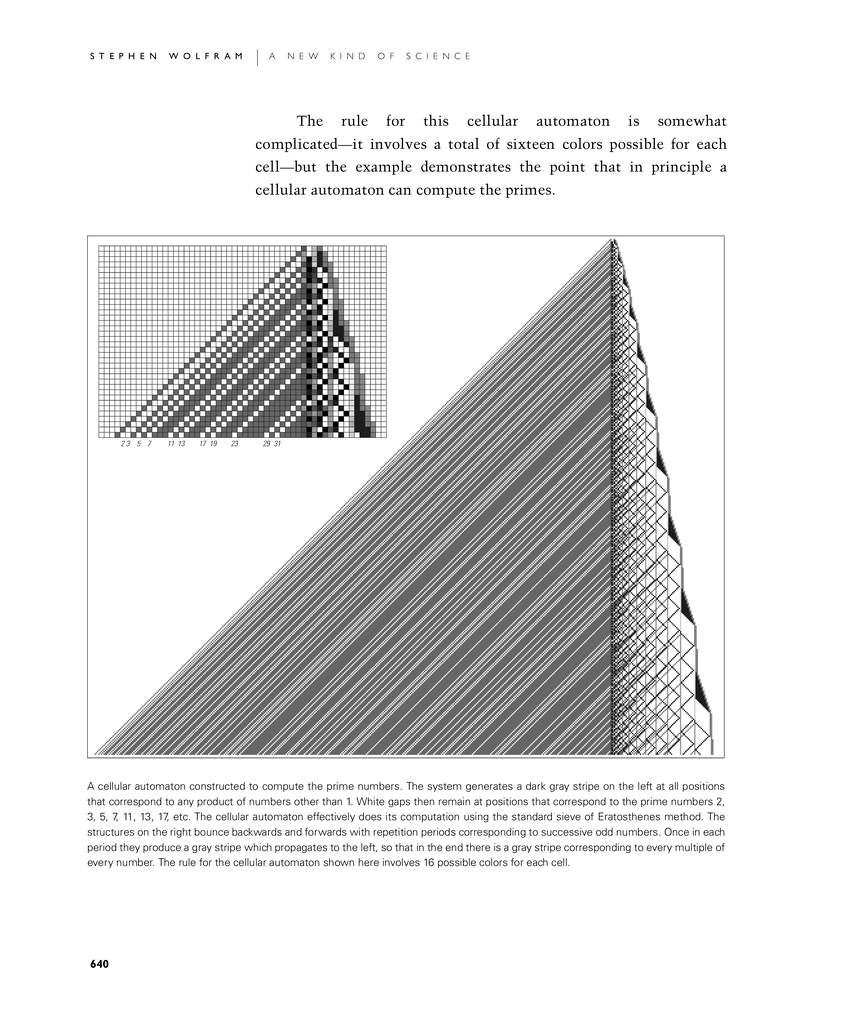
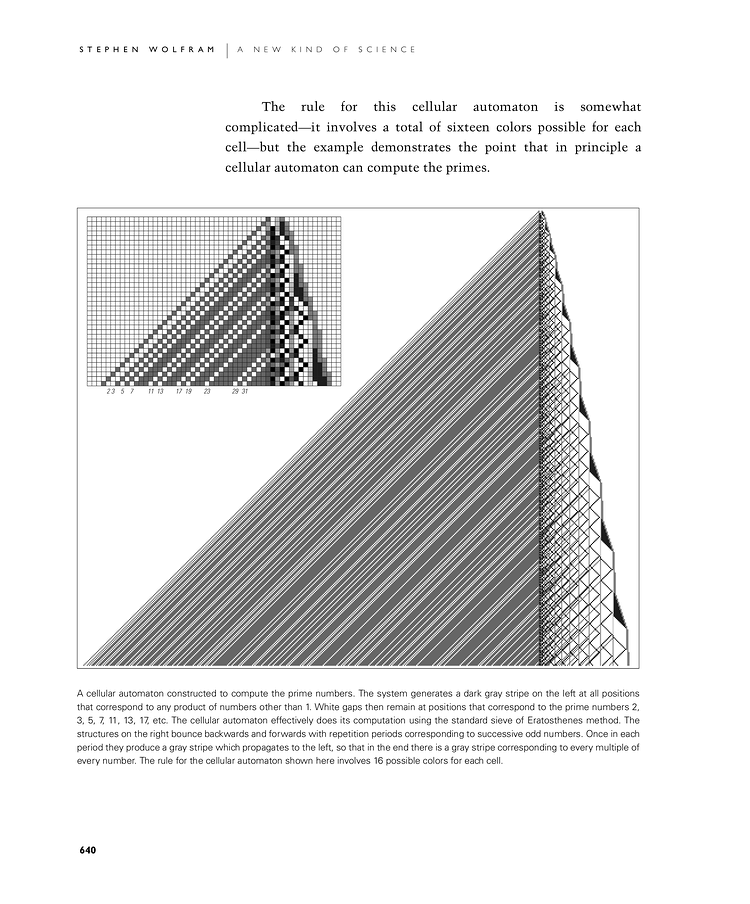
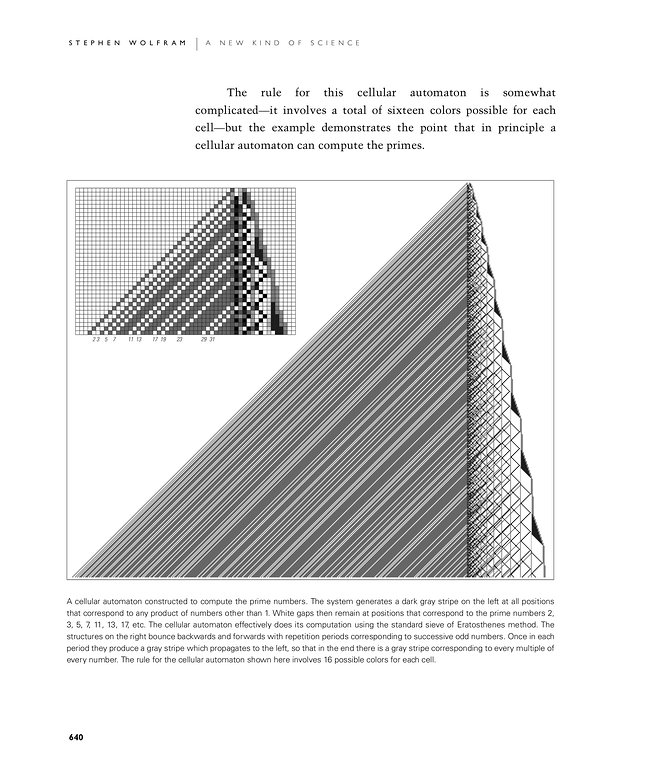
The rule for this cellular automaton is somewhat complicated—it involves a total of sixteen colors possible for each cell—but the example demonstrates the point that in principle a cellular automaton can compute the primes.

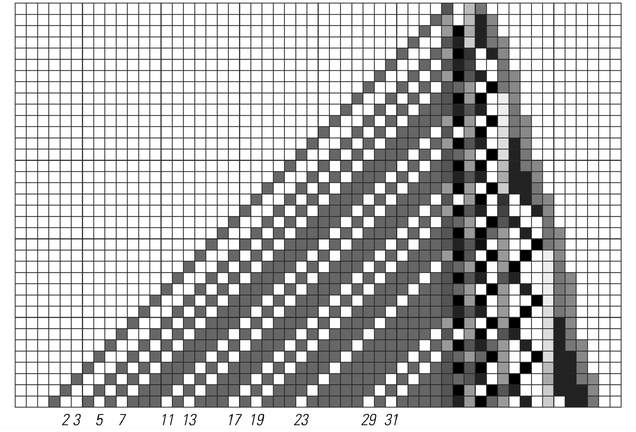
A cellular automaton constructed to compute the prime numbers. The system generates a dark gray stripe on the left at all positions that correspond to any product of numbers other than 1. White gaps then remain at positions that correspond to the prime numbers 2, 3, 5, 7, 11, 13, 17, etc. The cellular automaton effectively does its computation using the standard sieve of Eratosthenes method. The structures on the right bounce backwards and forwards with repetition periods corresponding to successive odd numbers. Once in each period they produce a gray stripe which propagates to the left, so that in the end there is a gray stripe corresponding to every multiple of every number. The rule for the cellular automaton shown here involves 16 possible colors for each cell.