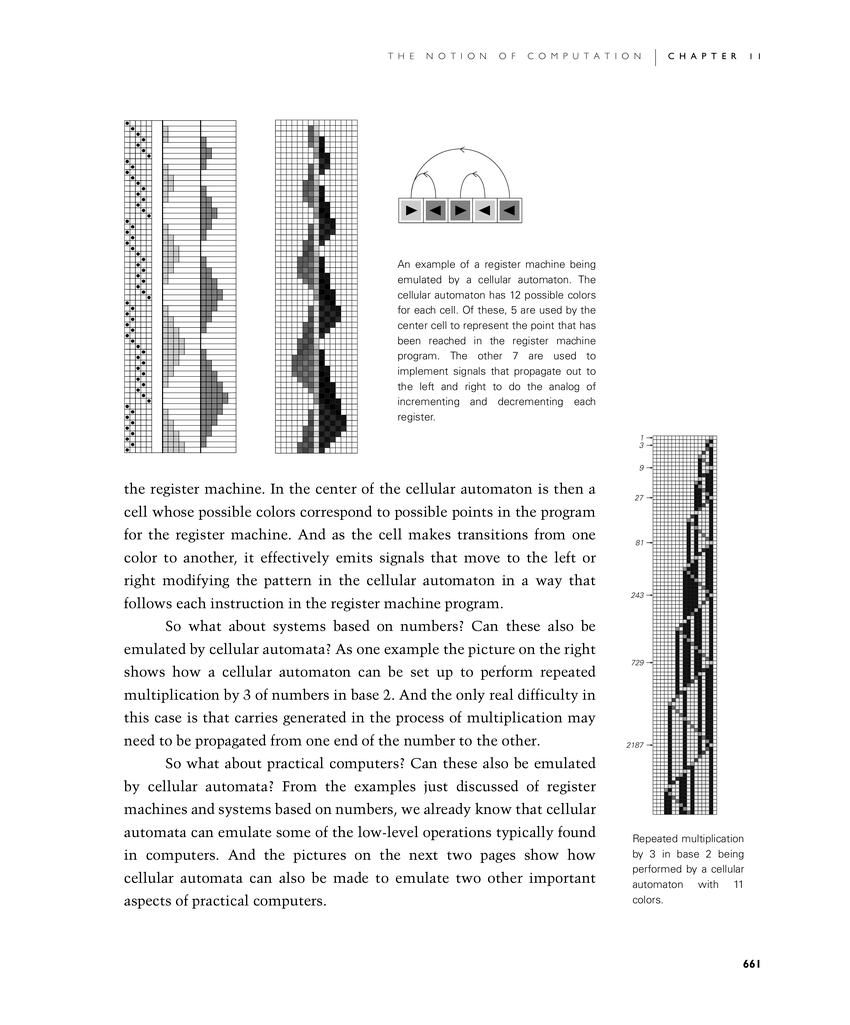
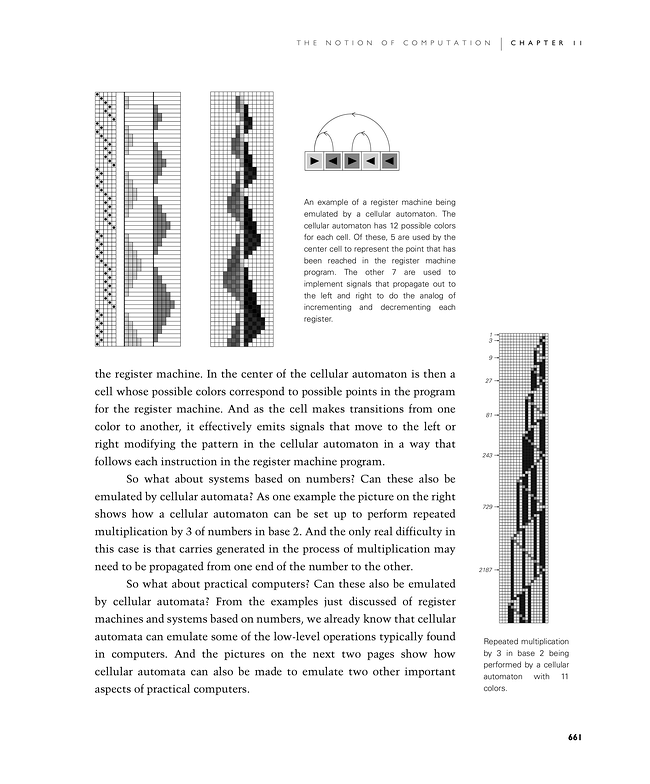
the register machine. In the center of the cellular automaton is then a cell whose possible colors correspond to possible points in the program for the register machine. And as the cell makes transitions from one color to another, it effectively emits signals that move to the left or right modifying the pattern in the cellular automaton in a way that follows each instruction in the register machine program.
So what about systems based on numbers? Can these also be emulated by cellular automata? As one example the bottom picture shows how a cellular automaton can be set up to perform repeated multiplication by 3 of numbers in base 2. And the only real difficulty in this case is that carries generated in the process of multiplication may need to be propagated from one end of the number to the other.
So what about practical computers? Can these also be emulated by cellular automata? From the examples just discussed of register machines and systems based on numbers, we already know that cellular automata can emulate some of the low-level operations typically found in computers. And the pictures on the next two pages [662, 663] show how cellular automata can also be made to emulate two other important aspects of practical computers.
 |  |
An example of a register machine being emulated by a cellular automaton. The cellular automaton has 12 possible colors for each cell. Of these, 5 are used by the center cell to represent the point that has been reached in the register machine program. The other 7 are used to implement signals that propagate out to the left and right to do the analog of incrementing and decrementing each register.
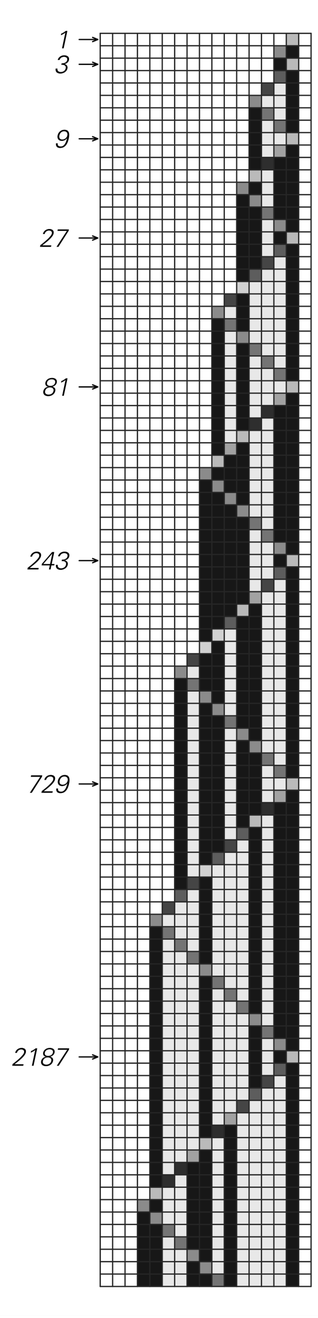
Repeated multiplication by 3 in base 2 being performed by a cellular automaton with 11 colors.