Continuing with the types of systems from the previous section, we come next to substitution systems. And here, for once, we find that at least at first we cannot in general emulate cellular automata. For as we discussed on page 83, neighbor-independent substitution systems can generate only patterns that are either repetitive or nested—so they can never yield the more complicated patterns that are, for example, needed to emulate rule 30.

But if one generalizes to neighbor-dependent substitution systems then it immediately becomes very straightforward to emulate cellular automata, as in the pictures below.

What about sequential substitution systems? Here again it turns out to be fairly easy to emulate cellular automata—as the pictures at the top of the facing page demonstrate.

Perhaps more surprisingly, the same is also true for ordinary tag systems. And even though such systems operate in an extremely simple underlying way, the pictures at the bottom of the facing page demonstrate that they can still quite easily emulate cellular automata.

What about symbolic systems? The structure of these systems is certainly vastly different from cellular automata. But once again—as the picture at the bottom of page 668 shows—it is quite easy to get these systems to emulate cellular automata.

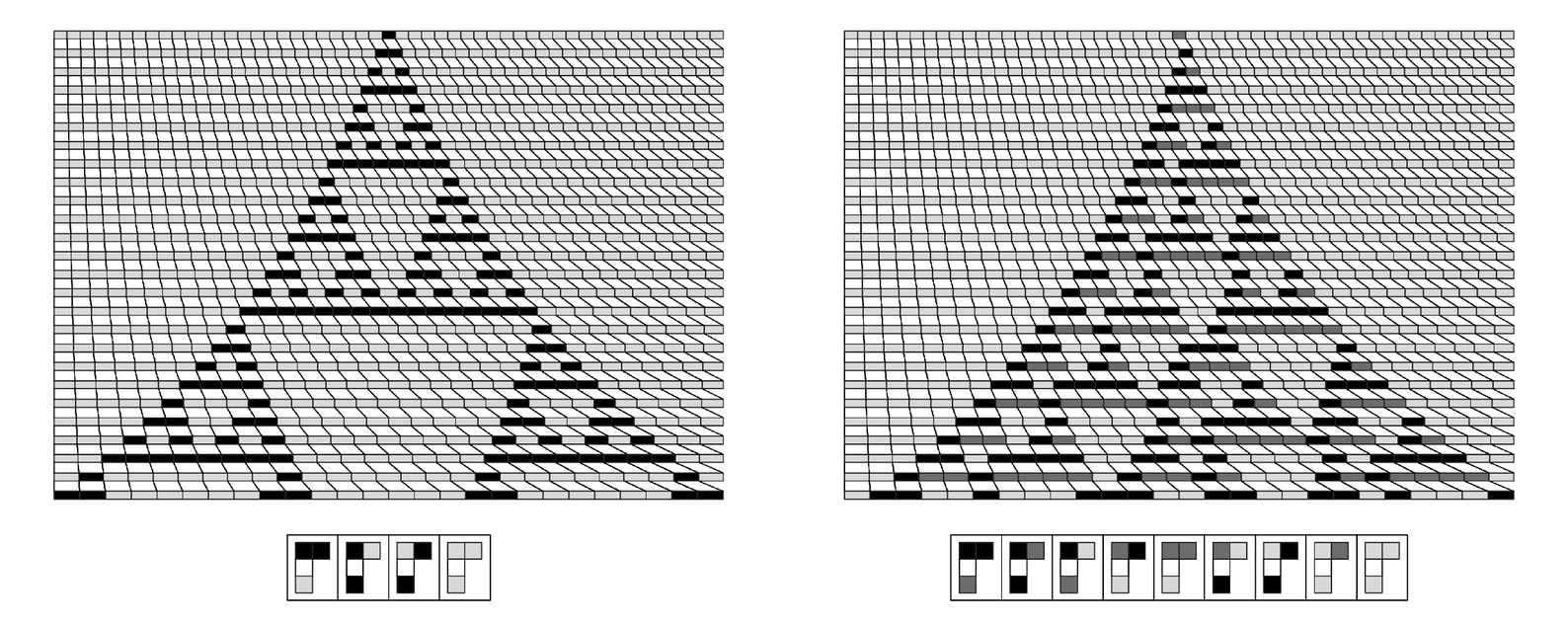
Neighbor-dependent substitution systems that emulate cellular automata with rules 90 and 30. The systems shown are simple examples of neighbor-dependent substitution systems with highly uniform rules always yielding just one cell and corresponding quite directly to cellular automata.