And as soon as one knows that any particular type of system is capable of emulating any cellular automaton, it immediately follows that there must be examples of that type of system that are universal.

So what about the other types of systems that we considered in Chapter 3? One that we have not yet discussed here are cyclic tag systems. And as it turns out, we will end up using just such systems later in this chapter as part of establishing a dramatic example of universality.

But to demonstrate that cyclic tag systems can manage to emulate cellular automata is not quite as straightforward as to do this for the various kinds of systems we have discussed so far. And indeed we will end up doing it in several stages. The first stage, illustrated in the top picture on the next page, is to get a cyclic tag system to emulate an ordinary tag system with the property that its rules depend only on the very first element that appears at each step.

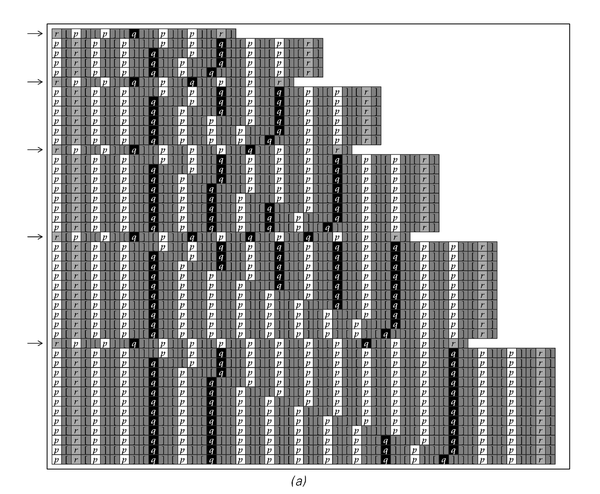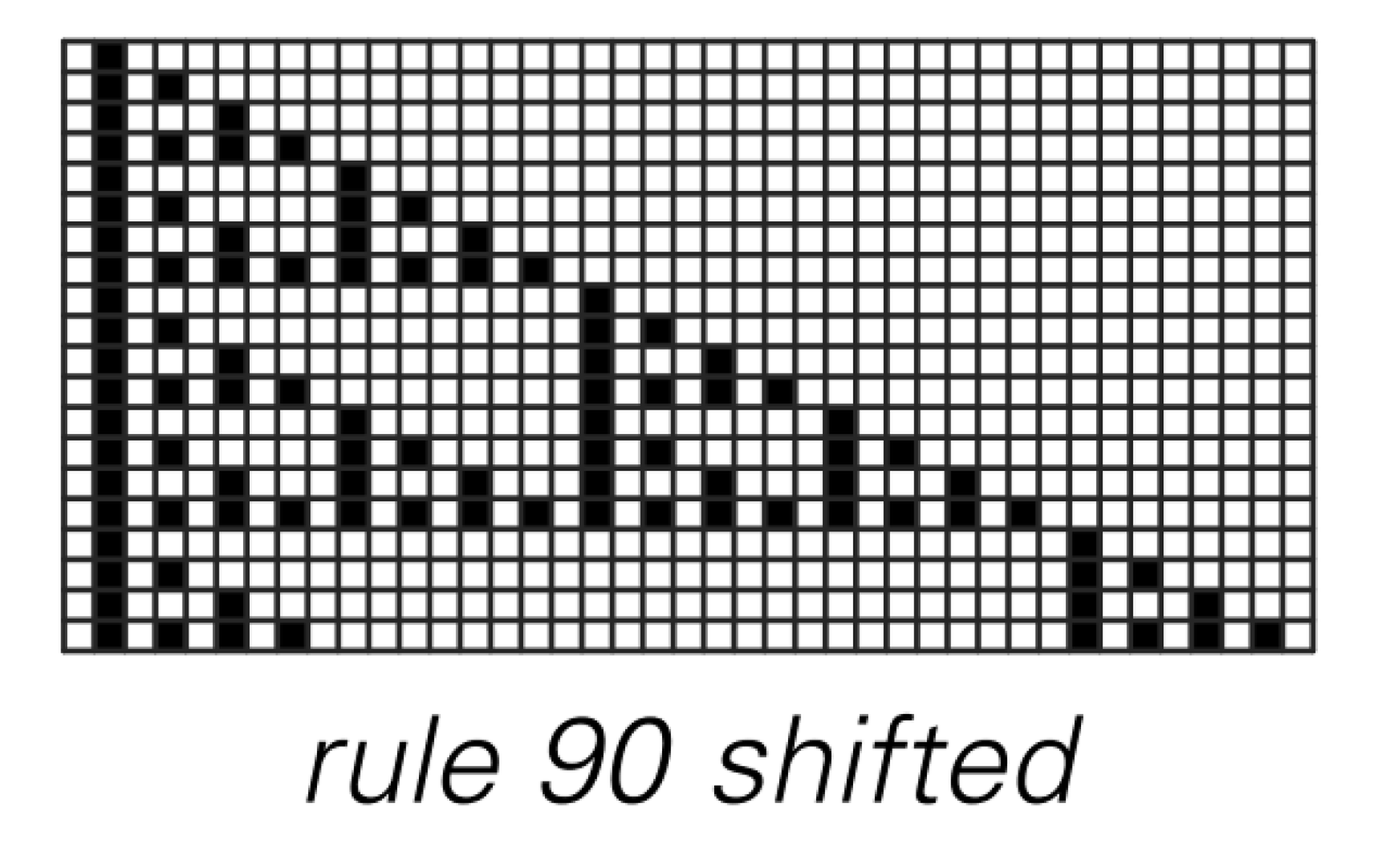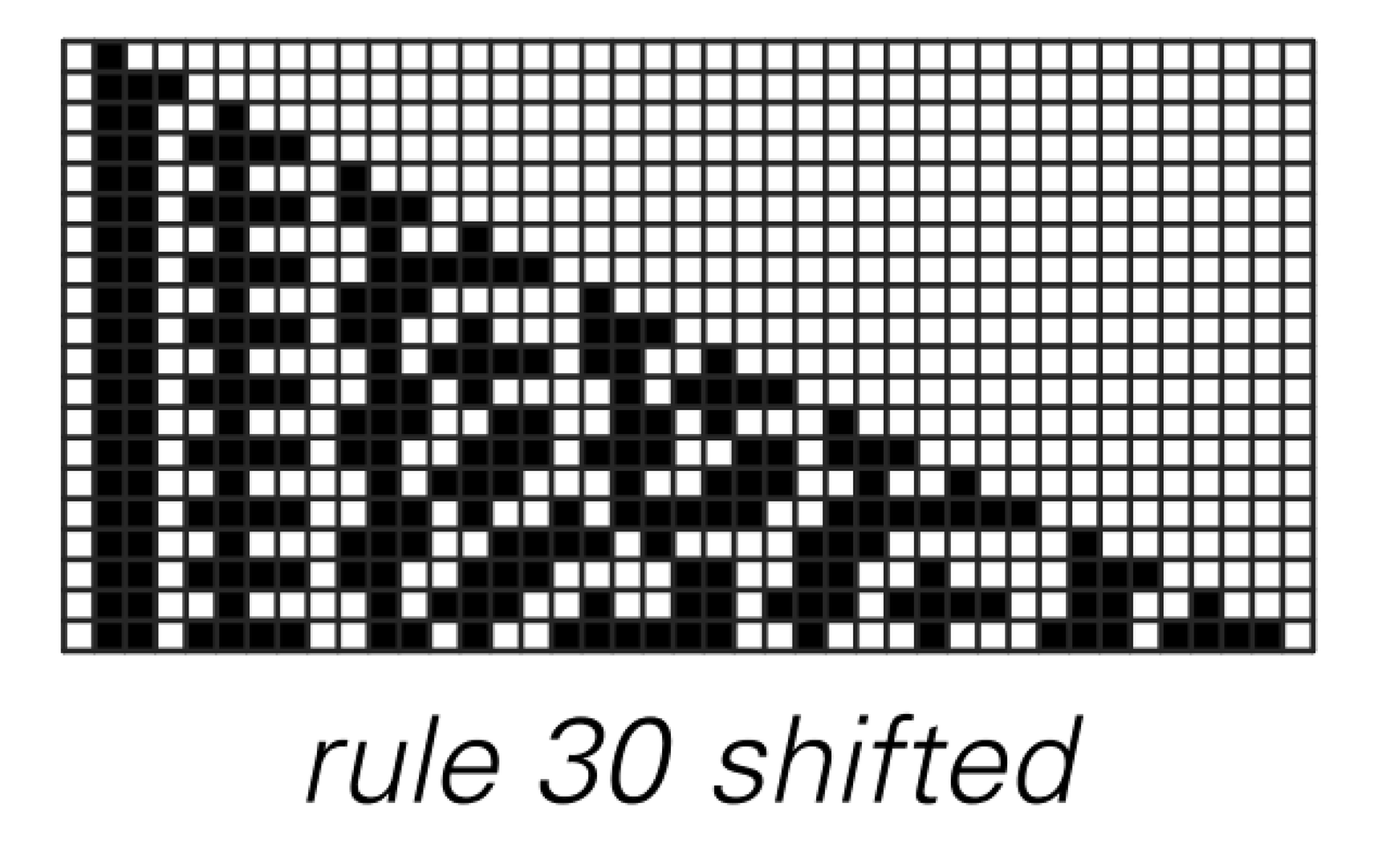Symbolic systems set up to emulate cellular automata that have rules 90 and 30. Unlike the examples of symbolic systems in Chapter 3, which involve only one symbol, these symbolic systems involve three symbols, p, q and r.