machine can readily be made to emulate a Turing machine with any number of colors. And through the construction of page 665 this then finally shows that a cyclic tag system can successfully emulate any cellular automaton—and can thus be universal.
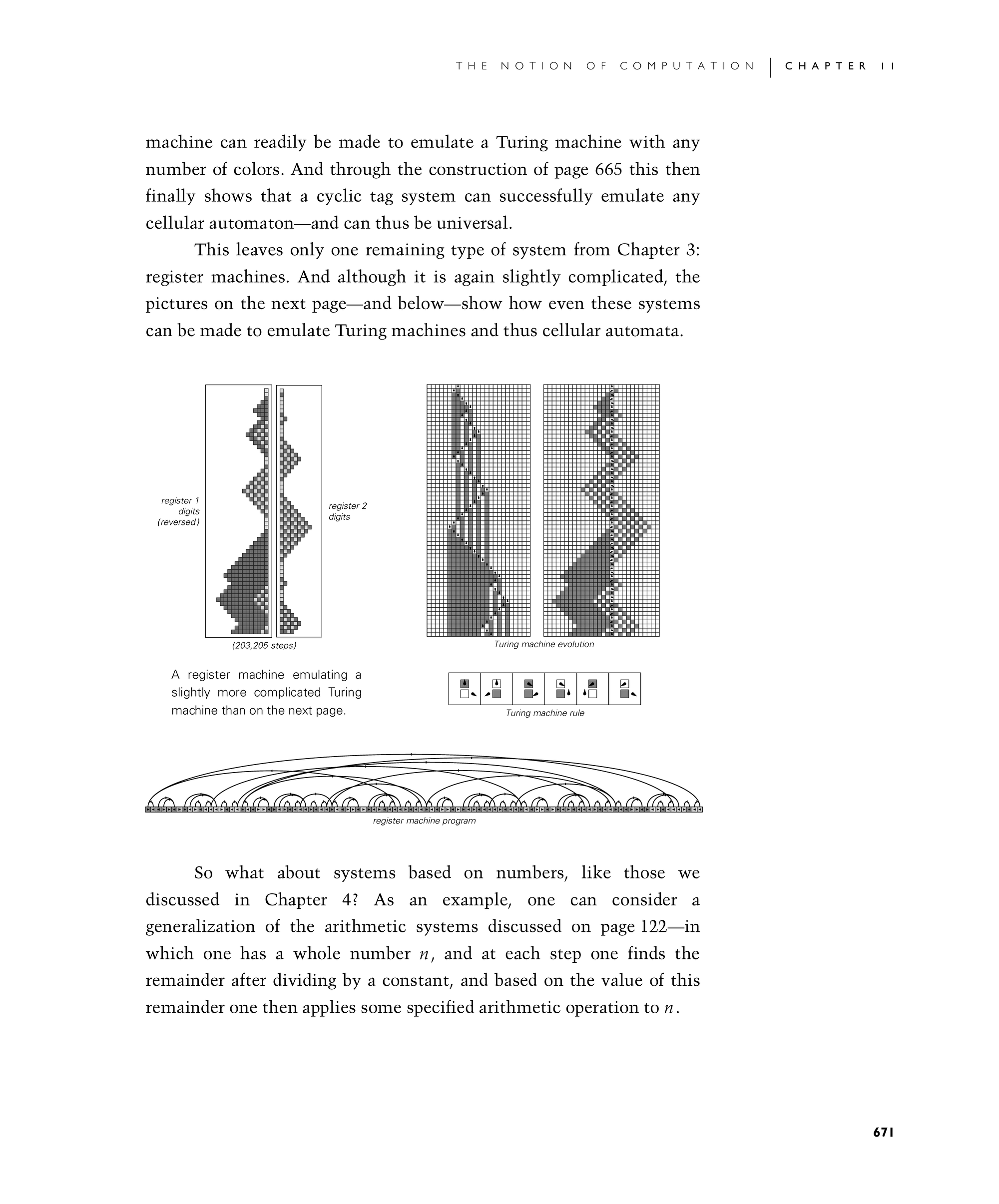
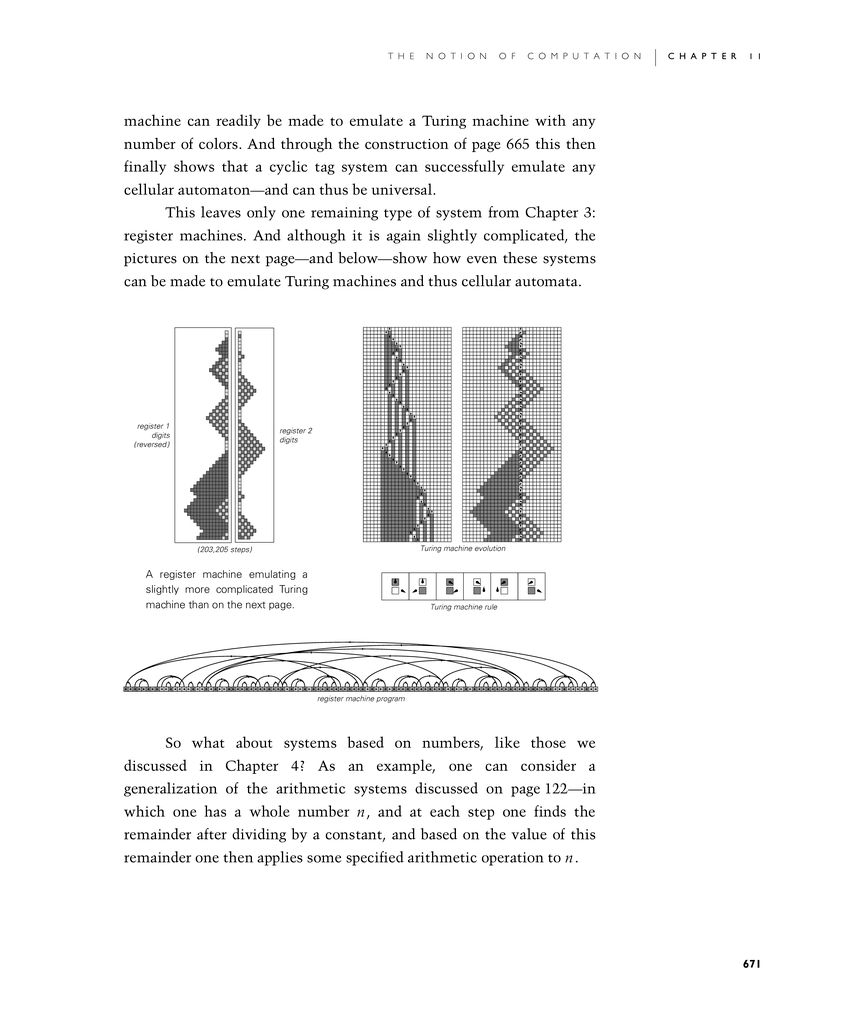
This leaves only one remaining type of system from Chapter 3: register machines. And although it is again slightly complicated, the pictures on the next page—and below—show how even these systems can be made to emulate Turing machines and thus cellular automata.
So what about systems based on numbers, like those we discussed in Chapter 4? As an example, one can consider a generalization of the arithmetic systems discussed on page 122—in which one has a whole number n, and at each step one finds the remainder after dividing by a constant, and based on the value of this remainder one then applies some specified arithmetic operation to n.
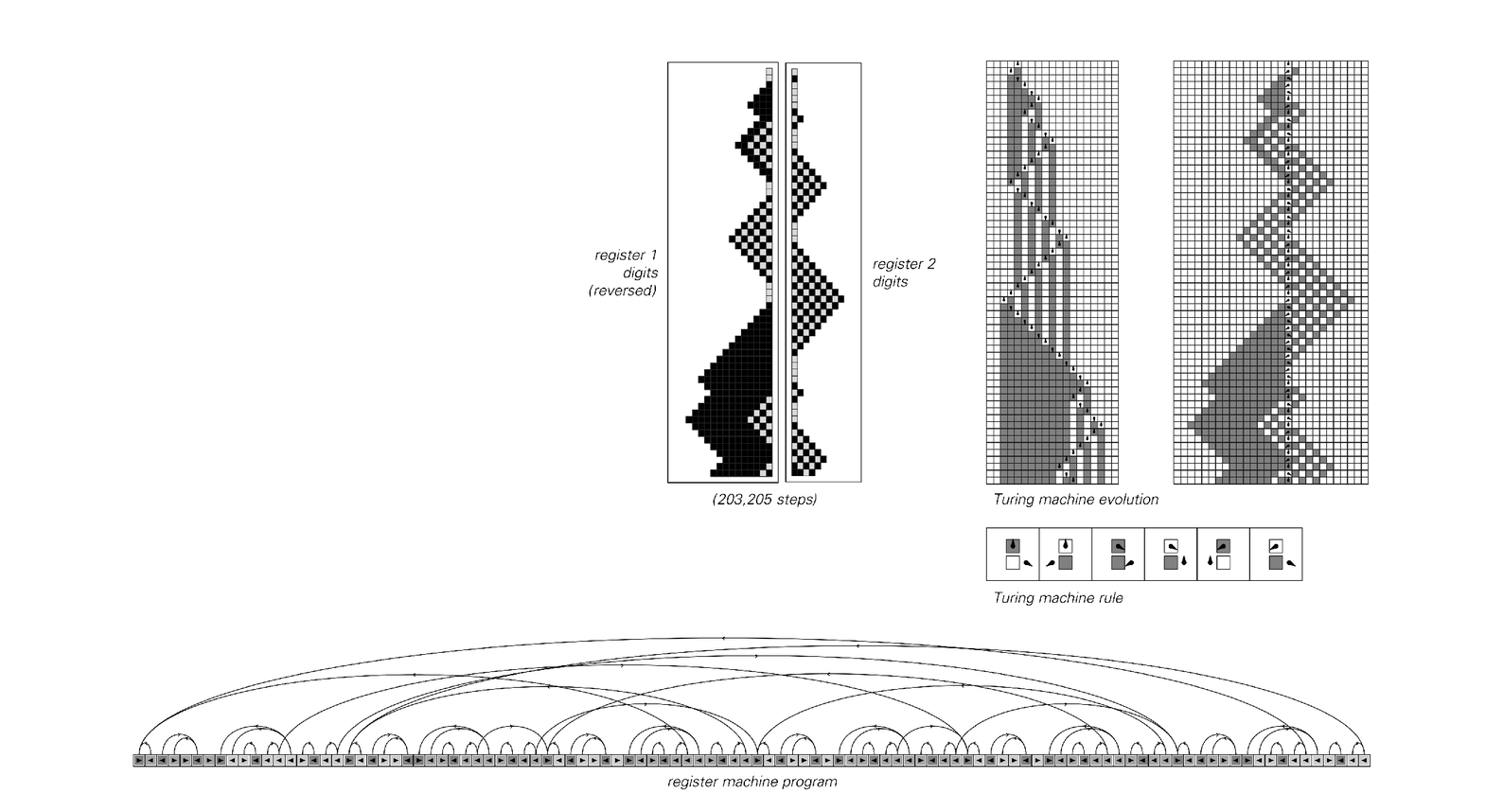
A register machine emulating a slightly more complicated Turing machine than on the next page.