The picture below shows that such a system can be set up to emulate a register machine. And from the fact that register machines are universal it follows that so too are such arithmetic systems.
And indeed the fact that it is possible to set up a universal system using essentially just the operations of ordinary arithmetic is closely related to the proof of Gödel's Theorem discussed on page 784.
But from what we have learned in this chapter, it no longer seems surprising that arithmetic should be capable of achieving universality. Indeed, considering all the kinds of systems that we have found can exhibit universality, it would have been quite peculiar if arithmetic had somehow not been able to support it.

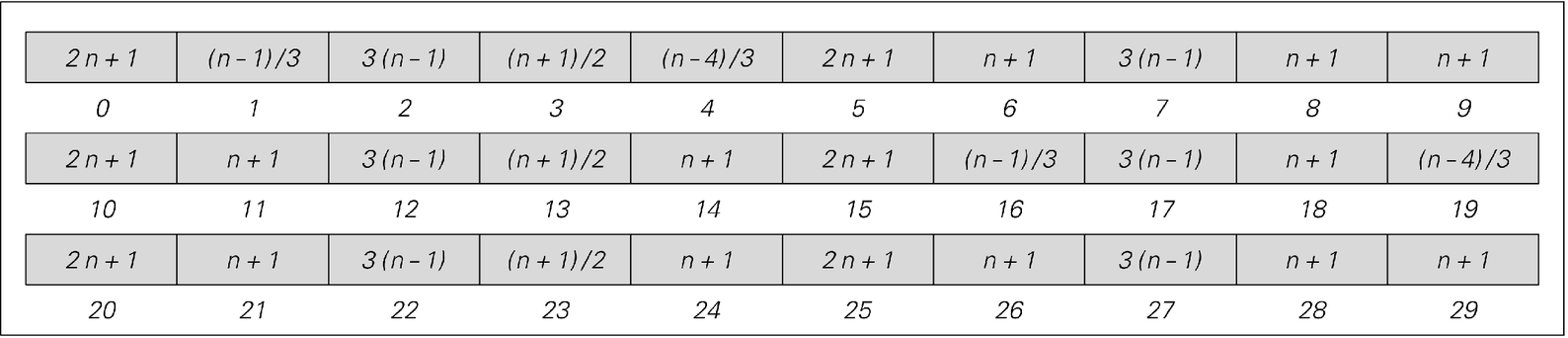
An example of how a simple arithmetic system can emulate a register machine. The arithmetic system takes the value n that it obtains at each step, computes Mod[n, 30], and then depending on the result applies to n one of the arithmetic operations specified by the rule above. The rule is set up so that if the value of n is written in the form i + 5, 2a, 3b then the values of i, a and b on successive steps correspond respectively to the position of the register machine in its program, and to the values of the two registers (2 and 3 appear because they are the first two primes; 5 appears because it is the length of the register machine program). The values of n in the pictures on the left are indicated on a logarithmic scale.



