Some localized structures are definitely seen. But are they enough to support class 4 behavior and universality? The pictures below show what happens if one starts looking in turn at each of the possible initial conditions for rule 54. At first one sees only simple repetitive behavior. At initial condition 291 one sees a very simple form of nesting. And as one continues one sees various other repetitive and nested forms. But at least up to the hundred millionth initial condition one sees nothing that is fundamentally any more complicated.
So can rule 54 achieve universality? I am not sure. It could be that if one went just a little further in looking at initial conditions one would see more complicated behavior. And it could be that even the structures shown above can be combined to produce all the richness that is needed for universality. But it could also be that whatever one does rule 54 will always in the end just show purely repetitive or nested behavior—which cannot on its own support universality.
What about other elementary cellular automata?
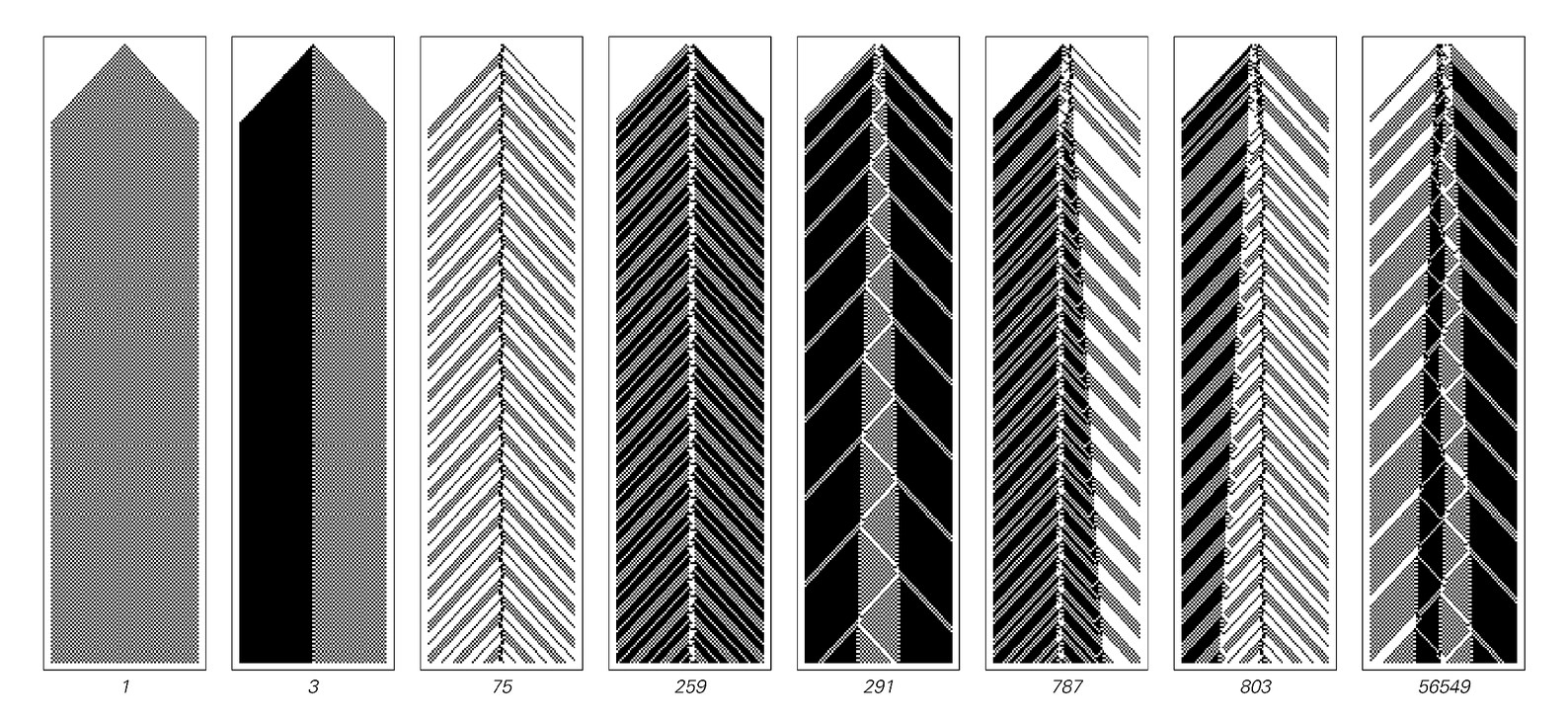
Forms of behavior seen in the first 100 million initial conditions for rule 54. With initial condition 291 the nth new stripe on the right is produced at step 2n2+8n-9. Even in the last case shown, the arrangement of stripes eventually becomes completely regular, with the nth new stripe being produced at step n2 + 21n/2 - {6, 5, -4, 3}〚Mod[n, 4] + 1〛/2. Pairs of cells are grouped together in each picture, as at the bottom of the facing page.



