input, and then to compute directly something that corresponds, say, to the outcome of that number of steps in the evolution of a system.
In traditional mathematics it is normally assumed that once one has an explicit formula involving standard mathematical functions then one can in effect always evaluate this formula immediately.
But evaluating a formula—like anything else—is a computational process. And unless some digits effectively never matter, this process cannot normally take less steps than there are digits in its input.
Indeed, it could in principle be that the process could take a number of steps proportional to the numerical value of its input. But if this were so, then it would mean that evaluating the formula would
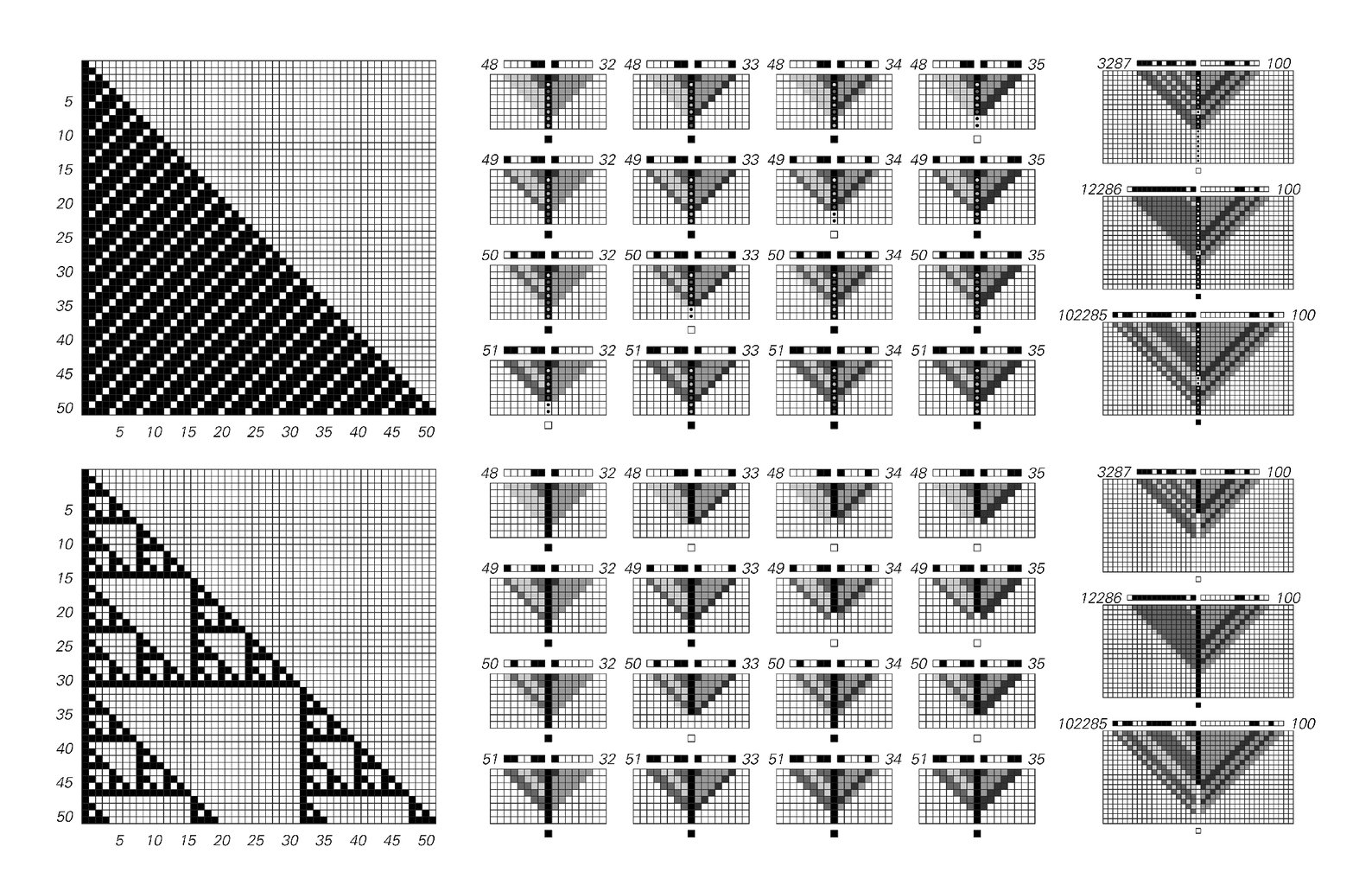
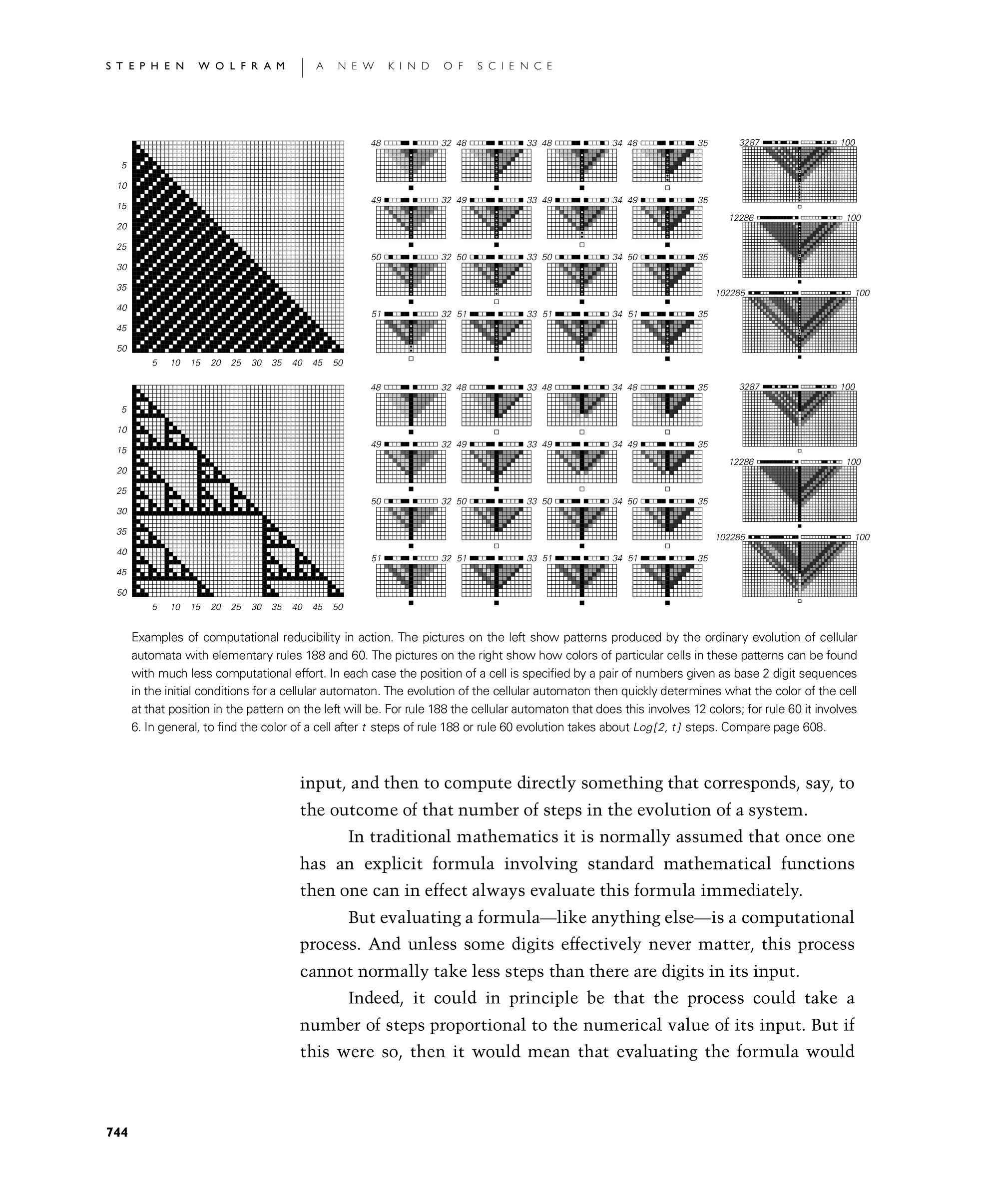
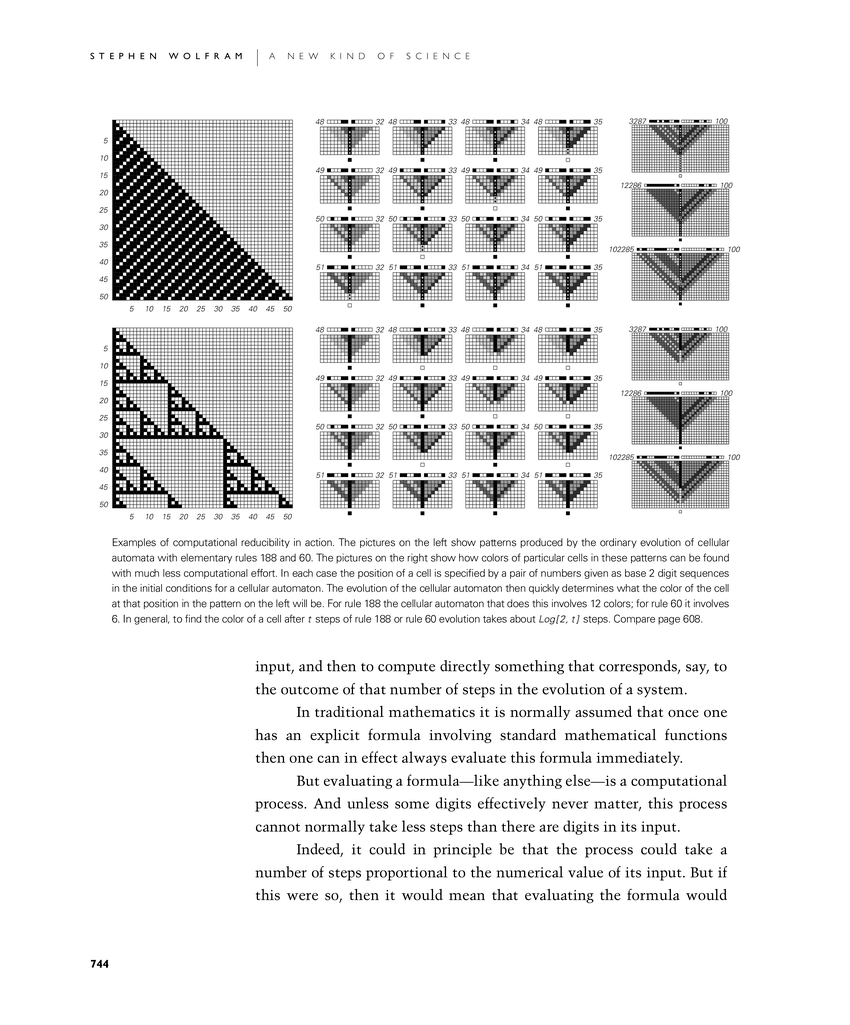
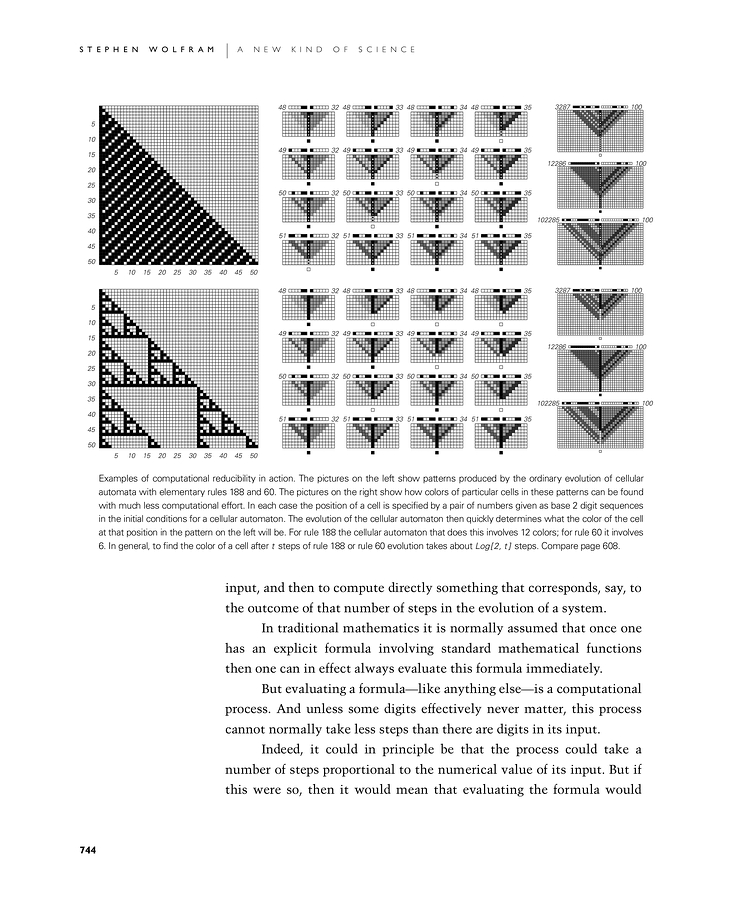
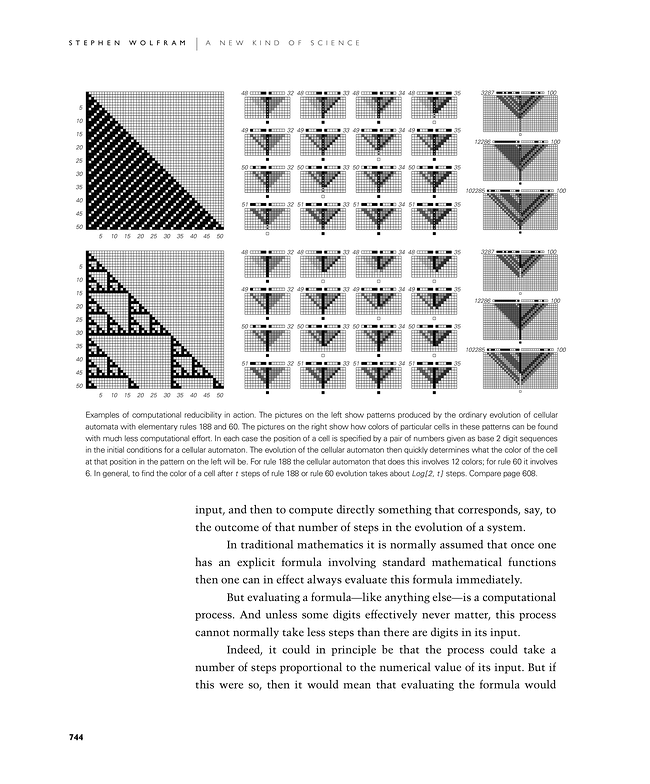
Examples of computational reducibility in action. The pictures on the left show patterns produced by the ordinary evolution of cellular automata with elementary rules 188 and 60. The pictures on the right show how colors of particular cells in these patterns can be found with much less computational effort. In each case the position of a cell is specified by a pair of numbers given as base 2 digit sequences in the initial conditions for a cellular automaton. The evolution of the cellular automaton then quickly determines what the color of the cell at that position in the pattern on the left will be. For rule 188 the cellular automaton that does this involves 12 colors; for rule 60 it involves 6. In general, to find the color of a cell after t steps of rule 188 or rule 60 evolution takes about Log[2, t] steps. Compare page 608.