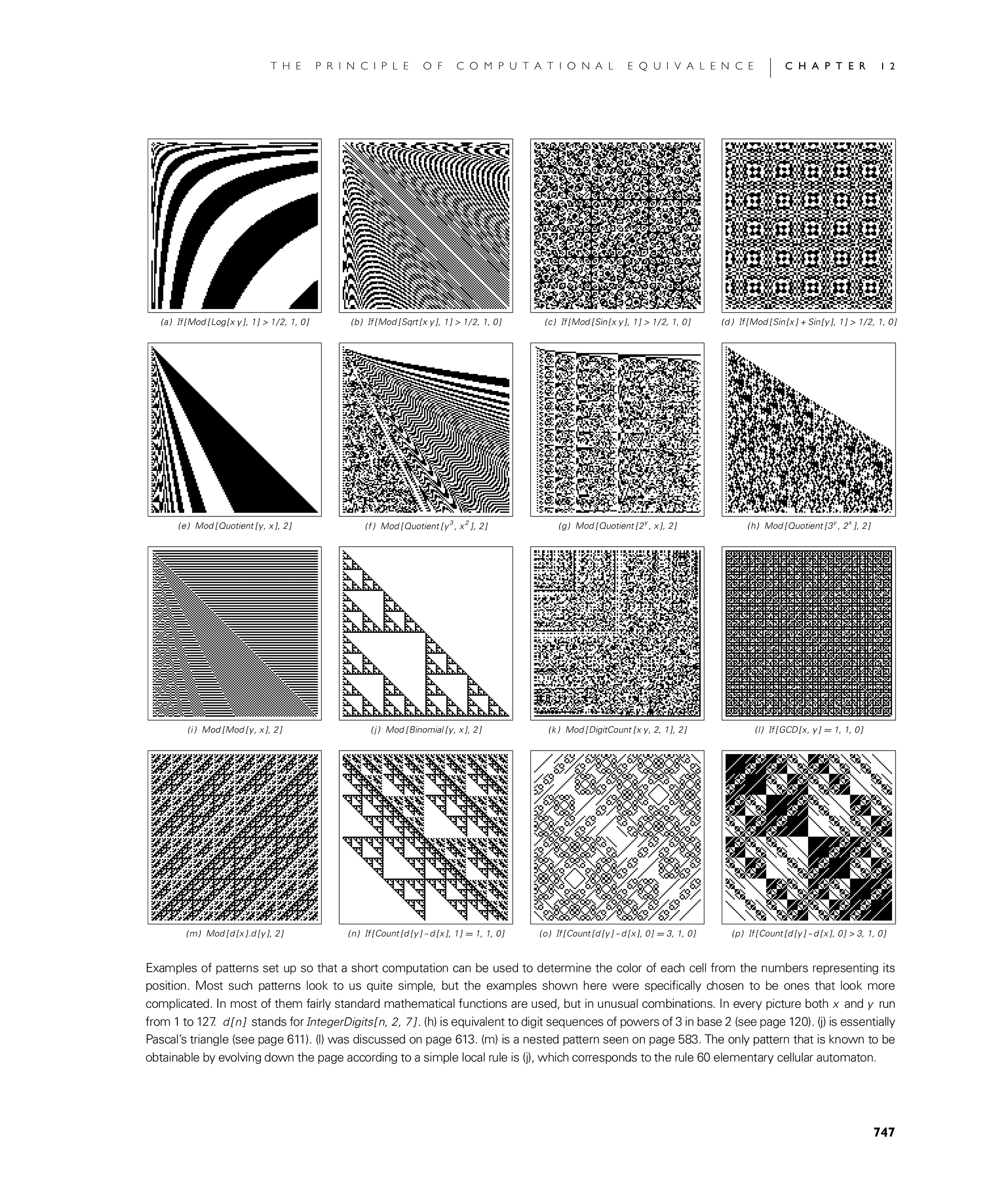
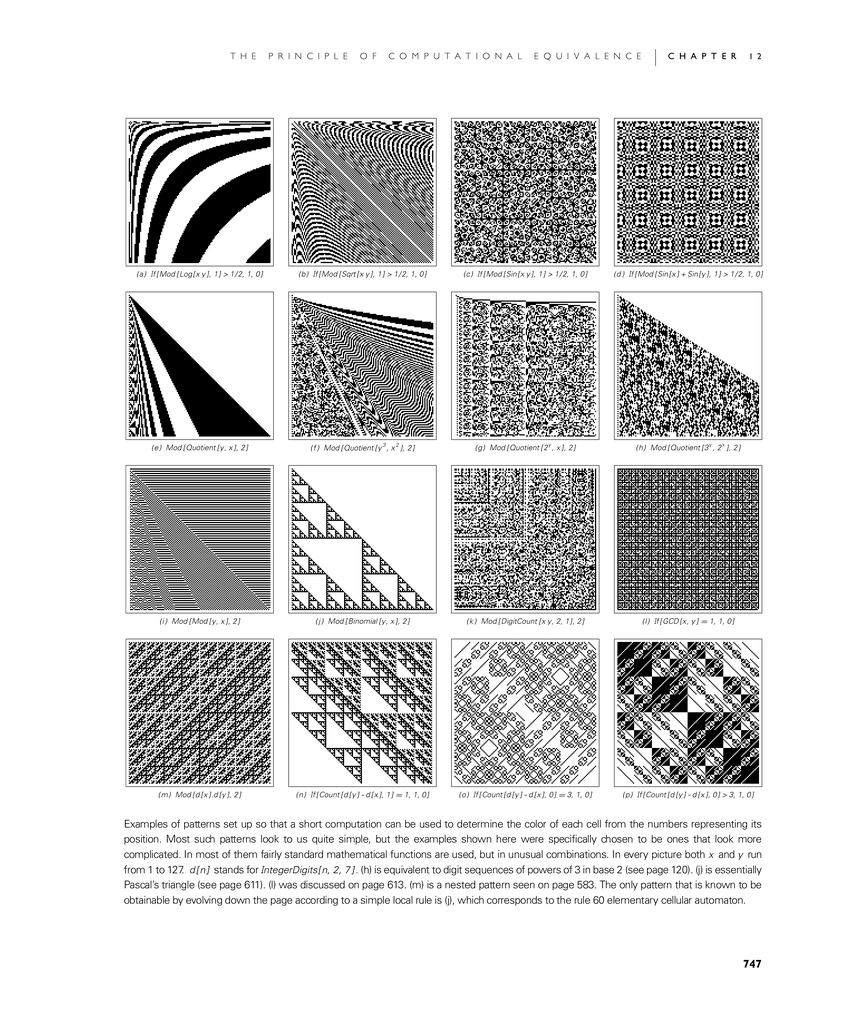
Examples of patterns set up so that a short computation can be used to determine the color of each cell from the numbers representing its position. Most such patterns look to us quite simple, but the examples shown here were specifically chosen to be ones that look more complicated. In most of them fairly standard mathematical functions are used, but in unusual combinations. In every picture both x and y run from 1 to 127. d[n] stands for IntegerDigits[n, 2, 7]. (h) is equivalent to digit sequences of powers of 3 in base 2 (see page 120). (j) is essentially Pascal's triangle (see page 611). (l) was discussed on page 613. (m) is a nested pattern seen on page 583. The only pattern that is known to be obtainable by evolving down the page according to a simple local rule is (j), which corresponds to the rule 60 elementary cellular automaton.