deterministic. But what the picture shows is that with successive initial conditions it emulates each possible path in the non-deterministic Turing machine.

And so what this means is that the problem of finding whether initial conditions exist that make the cellular automaton produce a certain outcome is equivalent to the non-deterministic Turing machine problem below—and is therefore in general NP-complete.

So what about other kinds of problems?

The picture on the next page shows the equivalence between the classic problem of satisfiability and the non-deterministic Turing machine problem below. In satisfiability what one does is to start with a collection of rows of black, white and gray squares. And then what one asks is whether any sequence of just black and

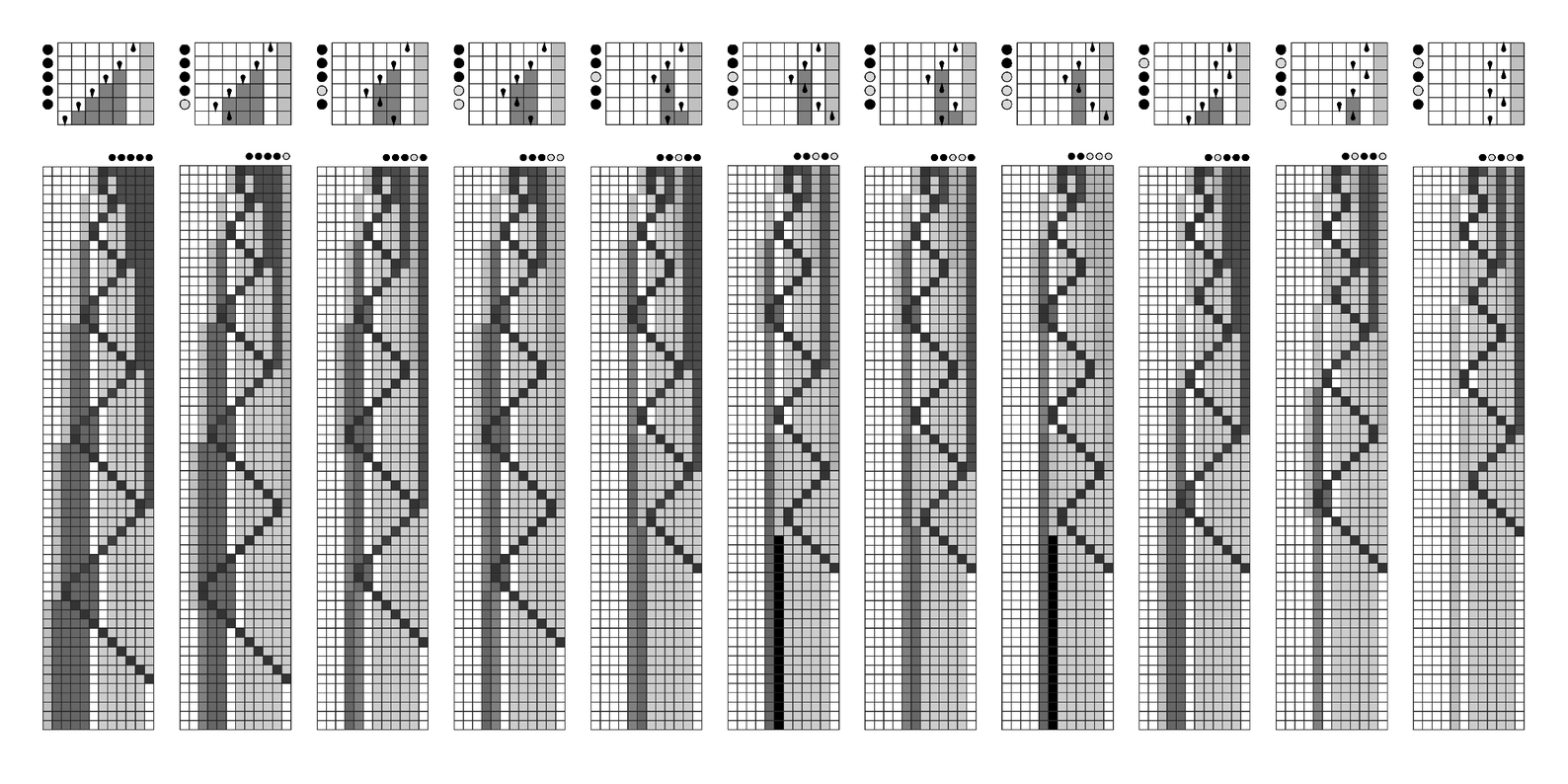
Translation between an NP-complete problem about non-deterministic Turing machines and about cellular automata. The top row shows how a particular non-deterministic Turing machine behaves with successive sequences of choices for rules to apply. The bottom row shows how a cellular automaton can be made to emulate this behavior when given a succession of different initial conditions. The cellular automaton is set up to produce a vertical black stripe if the head of the Turing machine ever goes further to the right than it starts—as it does in cases 6 and 8. The left part of each cellular automaton configuration emulates the actual evolution of the Turing machine; a specification of which rules should be applied at each step is progressively fetched from the right and delivered to the position of the head. Given particular initial conditions for the Turing machine the problem of whether the head ever goes further to the right than it starts is thus equivalent to the problem of whether the cellular automaton ever produces a vertical black stripe given particular initial conditions on its left. The cellular automaton takes 2t²+t steps to emulate t steps of evolution in the Turing machine. It involves a total of 19 colors.