In most kinds of mathematics there are all sorts of additional details, particularly about how to determine which parts of one or more previous expressions actually get used at each step in a proof. But much as in our study of systems in nature, one can try to capture the essential features of what can happen by using a simple idealized model.
And so for example one can imagine representing a step in a proof just by a string of simple elements such as black and white squares. And one can then consider the axioms of a system as defining possible transformations from one sequence of these elements to another—just like the rules in the multiway systems we discussed in Chapter 5.
The pictures below show how proofs of theorems work with this setup. Each theorem defines a connection between strings, and proving the theorem consists in finding a series of transformations—each associated with an axiom—that lead from one string to another.
But just as in the multiway systems in Chapter 5 one can also consider an explicit process of evolution, in which one starts from a
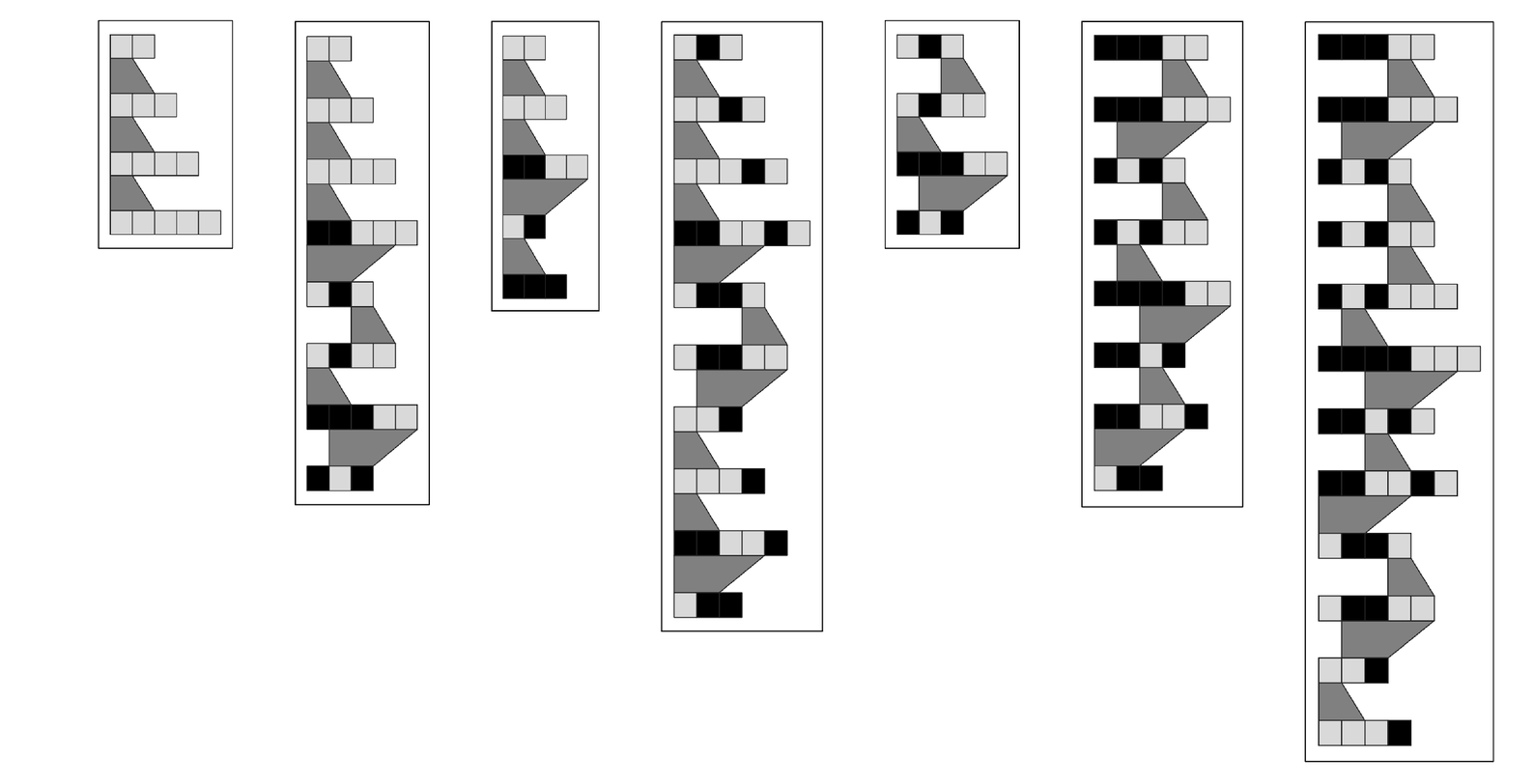
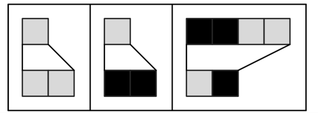
Simple idealizations of proofs in mathematics. The rules on the left in effect correspond to axioms that specify valid transformations between strings of black and white elements. The proofs above then show how one string—say ![]() —can be transformed into another—say
—can be transformed into another—say ![]() —by using the axioms. Typically there are many different proofs that can be given of a particular theorem; here in each case the ones shown are examples of the shortest possible proofs. The system shown is an example of a general substitution system of the kind discussed on page 497. Note that the fifth theorem
—by using the axioms. Typically there are many different proofs that can be given of a particular theorem; here in each case the ones shown are examples of the shortest possible proofs. The system shown is an example of a general substitution system of the kind discussed on page 497. Note that the fifth theorem ![]() ->
->![]() occurs in effect as a lemma in the second theorem
occurs in effect as a lemma in the second theorem ![]() ->
->![]() .
.



