particular string, then at each successive step one applies all possible transformations, so that in the end one builds up a whole network of connections between strings, as in the pictures below.
In a sense such a network can then be thought of as representing the whole field of mathematics that can be derived from whatever set of axioms one is using—with every connection between strings corresponding to a theorem, and every possible path to a proof.
But can networks like the ones below really reflect mathematics as it is actually practiced? For certainly the usual axioms in every traditional area of mathematics are significantly more complicated than any of the multiway system rules used below.
But just like in so many other cases in this book, it seems that even systems whose underlying rules are remarkably simple are already able to capture many of the essential features of mathematics.
An obvious observation in mathematics is that proofs can be difficult to do. One might at first assume that any theorem that is easy
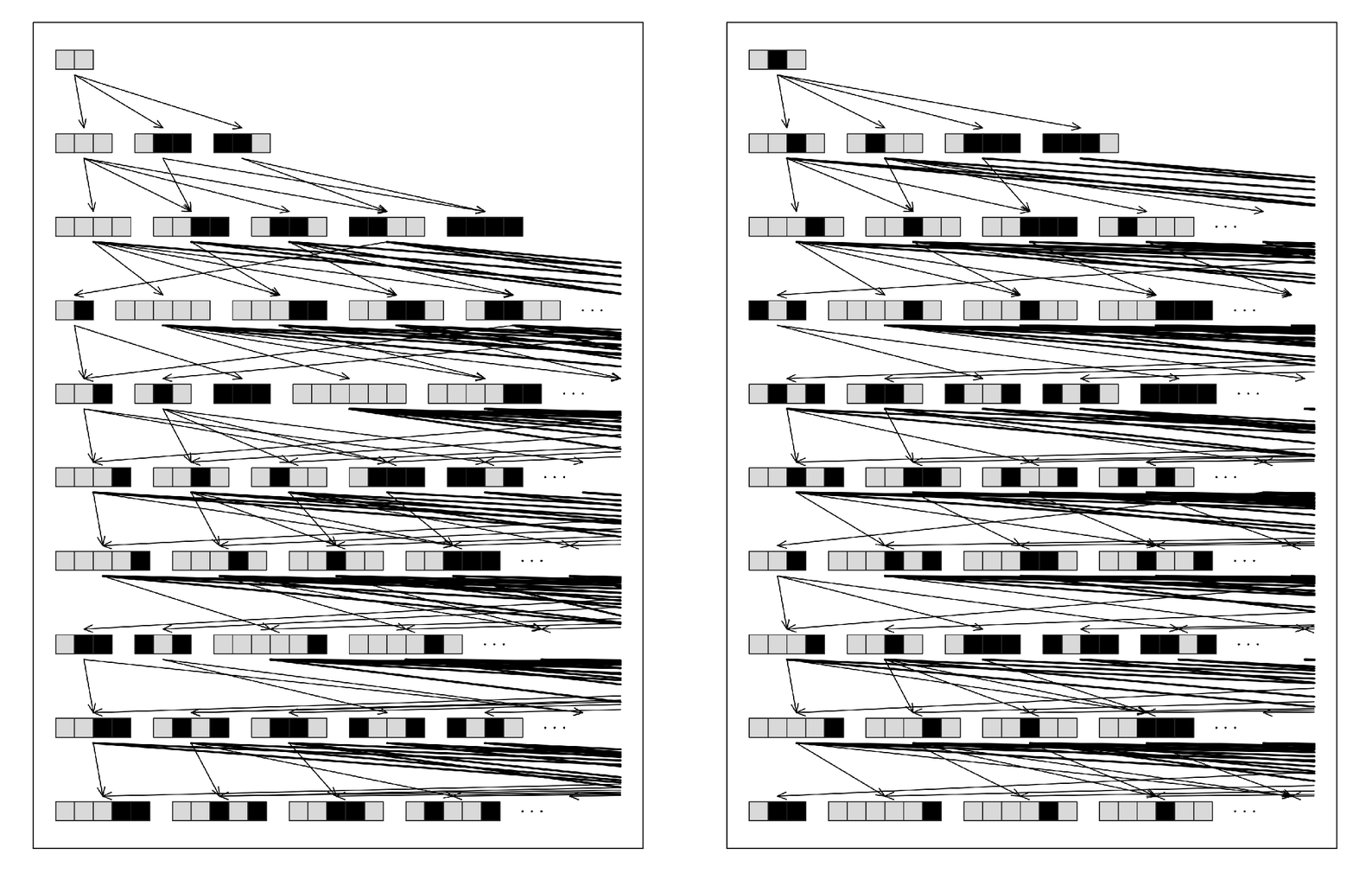
The result of applying the same transformations as on the facing page—but in all possible ways, corresponding to the evolution of a multiway system that represents all possible theorems that can be derived from the axioms. With the axioms used here, the total number of strings grows by a factor of roughly 1.7 at each step; on the last steps shown there are altogether 237 and 973 strings respectively.