any proof—regardless of length—exists for a specific result in a mathematical system with particular axioms.
So what are the implications of this?
Probably the most striking arise when one tries to apply traditional ideas of logic—and particularly notions of true and false.
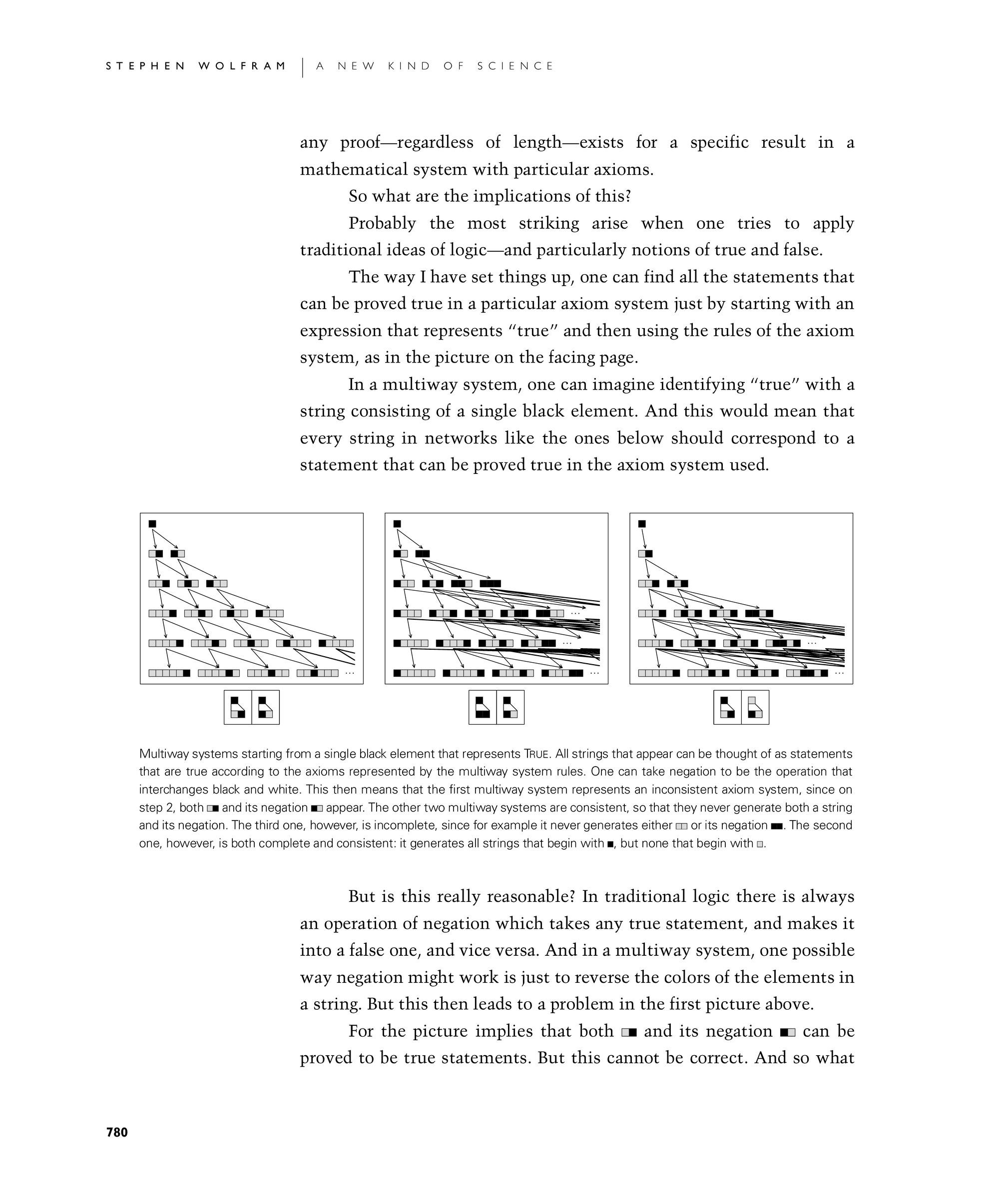
The way I have set things up, one can find all the statements that can be proved true in a particular axiom system just by starting with an expression that represents "true" and then using the rules of the axiom system, as in the picture on the facing page.
In a multiway system, one can imagine identifying "true" with a string consisting of a single black element. And this would mean that every string in networks like the ones below should correspond to a statement that can be proved true in the axiom system used.
But is this really reasonable? In traditional logic there is always an operation of negation which takes any true statement, and makes it into a false one, and vice versa. And in a multiway system, one possible way negation might work is just to reverse the colors of the elements in a string. But this then leads to a problem in the first picture below.
For the picture implies that both
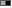 and its negation
and its negation 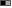 can be proved to be true statements. But this cannot be correct. And so what
can be proved to be true statements. But this cannot be correct. And so what
Multiway systems starting from a single black element that represents True. All strings that appear can be thought of as statements that are true according to the axioms represented by the multiway system rules. One can take negation to be the operation that interchanges black and white. This then means that the first multiway system represents an inconsistent axiom system, since on step 2, both ![]() and its negation
and its negation ![]() appear. The other two multiway systems are consistent, so that they never generate both a string and its negation. The third one, however, is incomplete, since for example it never generates either
appear. The other two multiway systems are consistent, so that they never generate both a string and its negation. The third one, however, is incomplete, since for example it never generates either ![]() or its negation
or its negation ![]() . The second one, however, is both complete and consistent: it generates all strings that begin with
. The second one, however, is both complete and consistent: it generates all strings that begin with ![]() , but none that begin with
, but none that begin with ![]() .
.