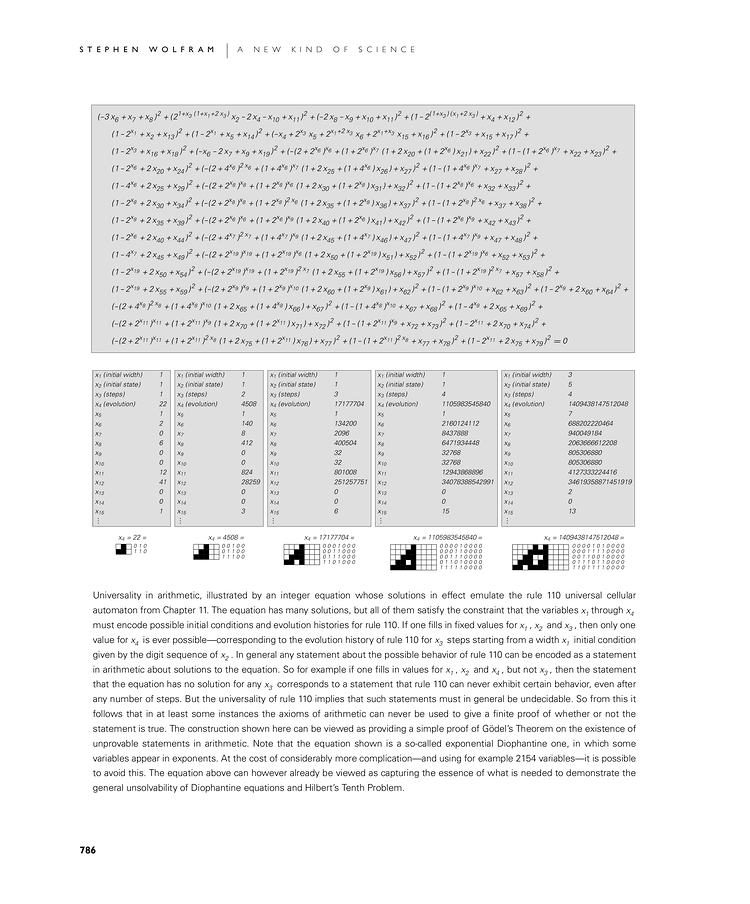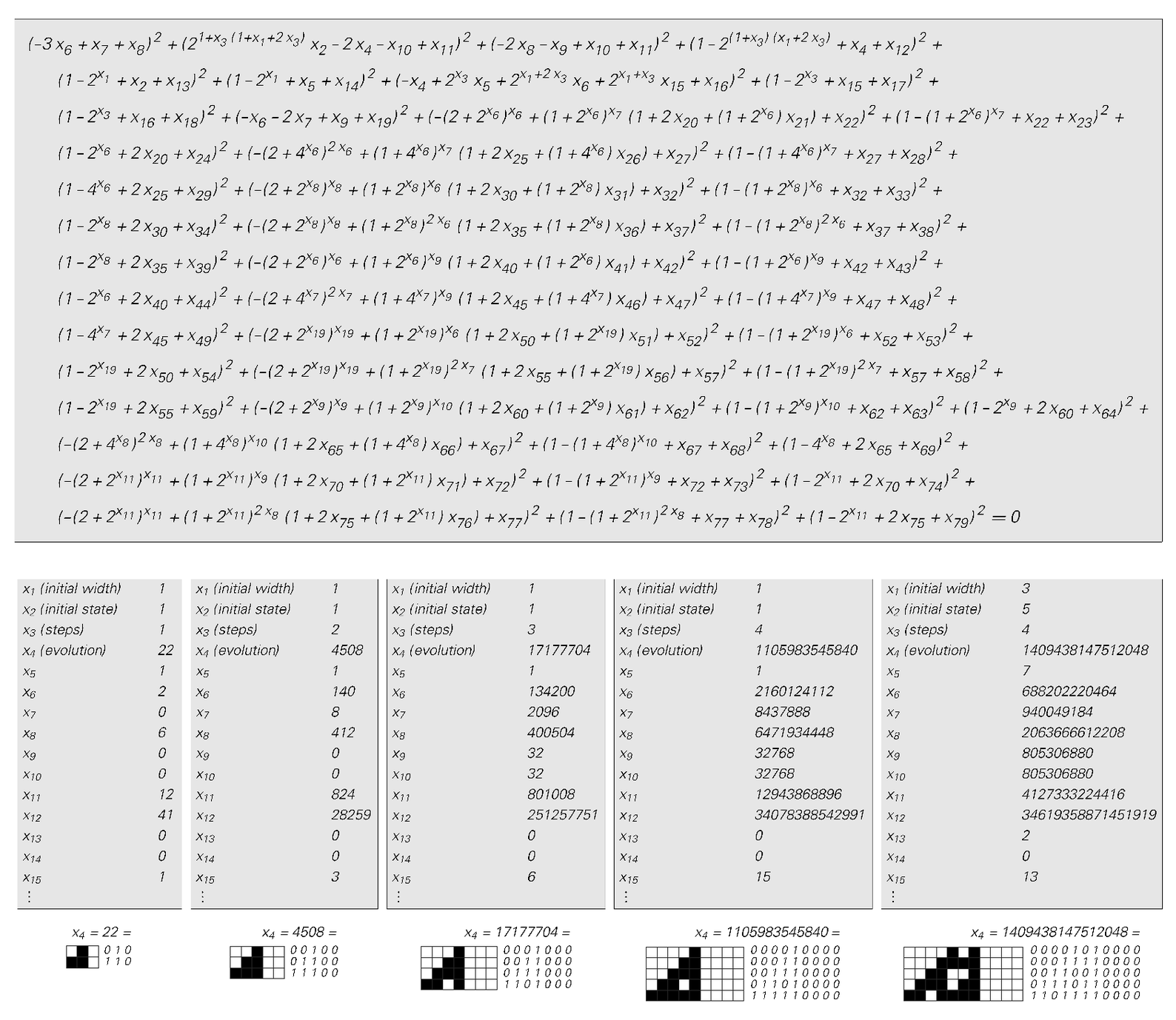
Universality in arithmetic, illustrated by an integer equation whose solutions in effect emulate the rule 110 universal cellular automaton from Chapter 11. The equation has many solutions, but all of them satisfy the constraint that the variables x1 through x4 must encode possible initial conditions and evolution histories for rule 110. If one fills in fixed values for x1, x2 and x3, then only one value for x4 is ever possible—corresponding to the evolution history of rule 110 for x3 steps starting from a width x1 initial condition given by the digit sequence of x2. In general any statement about the possible behavior of rule 110 can be encoded as a statement in arithmetic about solutions to the equation. So for example if one fills in values for x1, x2 and x4, but not x3, then the statement that the equation has no solution for any x3 corresponds to a statement that rule 110 can never exhibit certain behavior, even after any number of steps. But the universality of rule 110 implies that such statements must in general be undecidable. So from this it follows that in at least some instances the axioms of arithmetic can never be used to give a finite proof of whether or not the statement is true. The construction shown here can be viewed as providing a simple proof of Gödel's Theorem on the existence of unprovable statements in arithmetic. Note that the equation shown is a so-called exponential Diophantine one, in which some variables appear in exponents. At the cost of considerably more complication—and using for example 2154 variables—it is possible to avoid this. The equation above can however already be viewed as capturing the essence of what is needed to demonstrate the general unsolvability of Diophantine equations and Hilbert's Tenth Problem.