But in fact, in the fifteen years or so since I first emphasized the importance of cellular automata all sorts of traditional mathematical work has actually been done on them. So how has this been possible?
The basic point is that the work has tended to concentrate on particular aspects of cellular automata that are simple enough to avoid undecidability and unprovability. And typically it has achieved this in one of two ways: either by considering only very specific cases that have been observed or constructed to be simple, or by looking at things in so much generality that only rather simple properties ever survive.
So for example when presented with the 256 elementary cellular automaton patterns shown on page 55 mathematicians in my experience have two common responses: either to single out specific patterns that have a simple repetitive or perhaps nested form, or to generalize and look not at individual patterns, but rather at aggregate properties obtained say by evolving from all possible initial conditions.
And about questions that concern, for example, the structure of a pattern that looks to us complex, the almost universal reaction is that such questions can somehow not be of any real mathematical interest.
Needless to say, in the framework of the new kind of science in this book, such questions are now of great interest. And my results

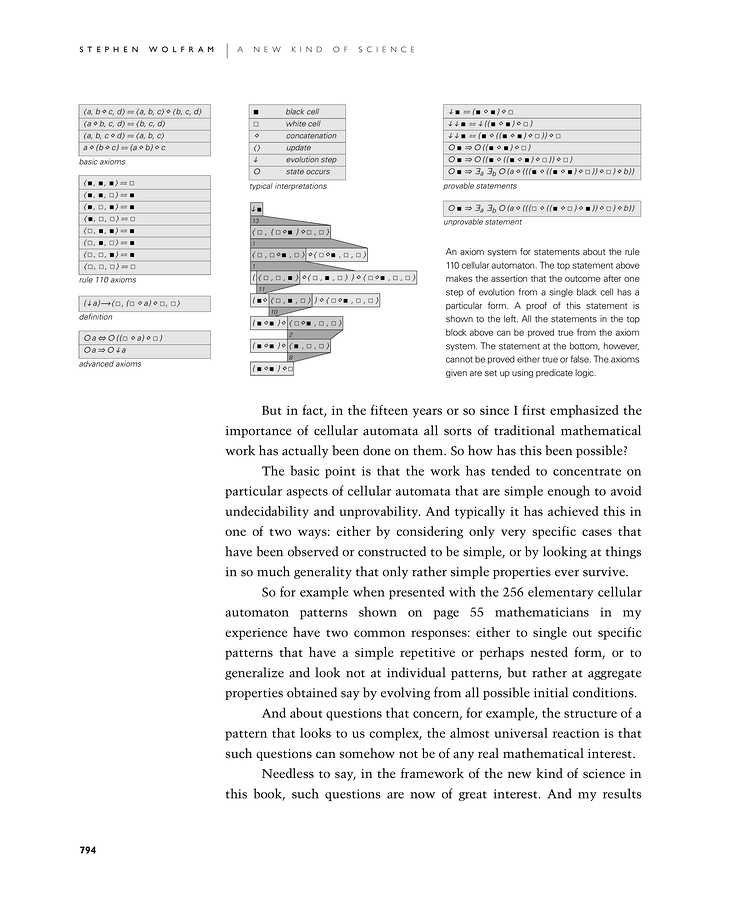
An axiom system for statements about the rule 110 cellular automaton. The top statement on the right makes the assertion that the outcome after one step of evolution from a single black cell has a particular form. A proof of this statement is shown to the left. All the statements in the top block above can be proved true from the axiom system. The bottom-right statement, however, cannot be proved either true or false. The axioms given are set up using predicate logic.