But to formulate such a question in a meaningful way one needs a notion of negation. In general, negation is just some operation that takes a string and yields another, giving back the original if it is applied a second time. Earlier in this section we discussed cases in which negation simply reverses the color of each element in a string. And as a generalization of this one can consider cases in which negation can be any operation that preserves lengths of strings.

And in this case it turns out that the criterion for whether a system is complete and consistent is simply that exactly half the

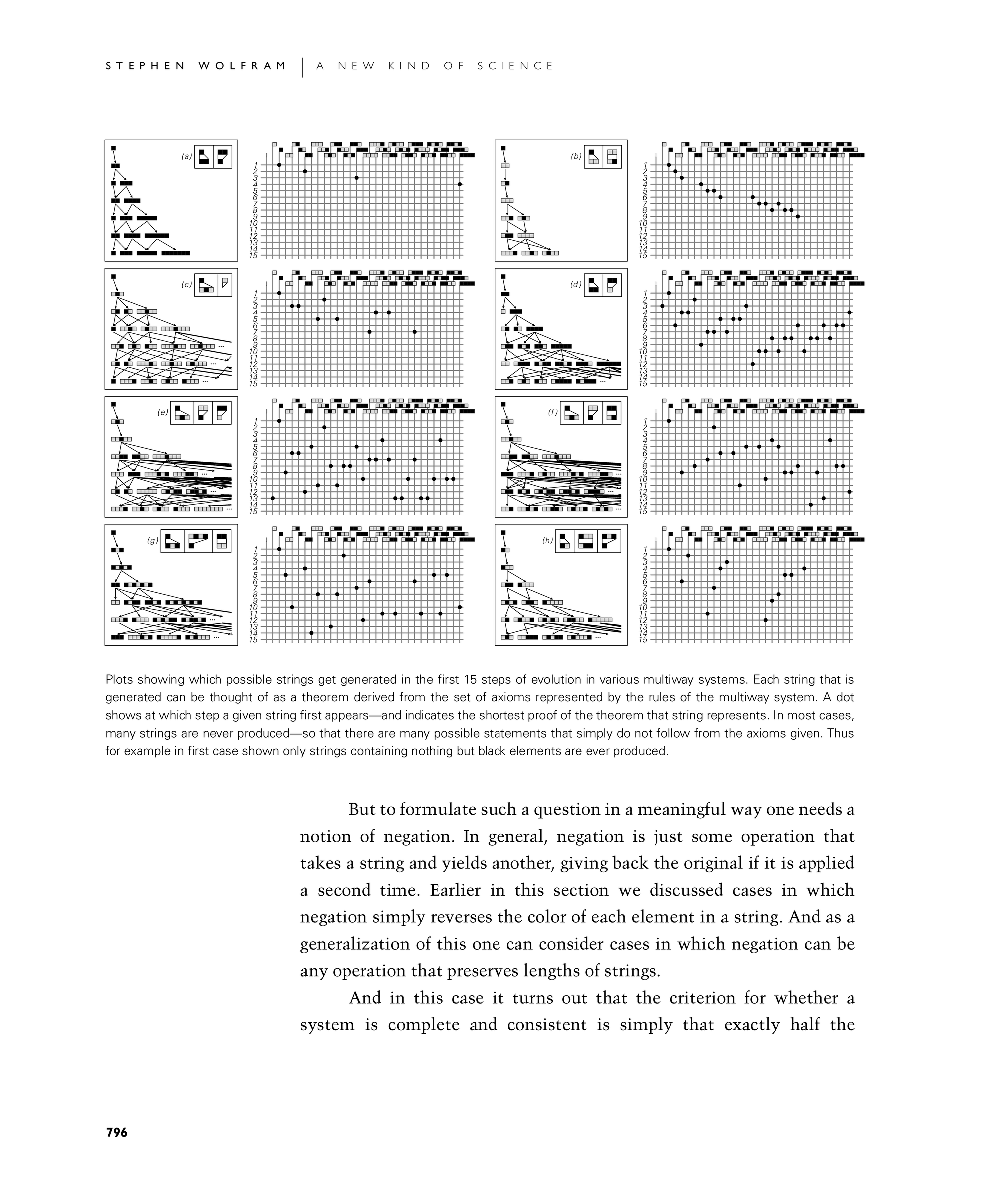
Plots showing which possible strings get generated in the first 15 steps of evolution in various multiway systems. Each string that is generated can be thought of as a theorem derived from the set of axioms represented by the rules of the multiway system. A dot shows at which step a given string first appears—and indicates the shortest proof of the theorem that string represents. In most cases, many strings are never produced—so that there are many possible statements that simply do not follow from the axioms given. Thus for example in first case shown only strings containing nothing but black elements are ever produced.