and Nor. And this means that it cannot successfully reproduce all the results of logic. Yet if any axiom system with just a single axiom is going to be able to do this, the axiom must be of the form {… a}.
With up to 6 Nands and 2 variables none of the 16,896 possible axiom systems of this kind work even up to 3-value operators. But with 6 Nands and 3 variables, 296 of the 288,684 possible axiom systems work up to 3-value operators, and 100 work up to 4-value operators.
And of the 25 of these that are not trivially equivalent, it then turns out that the two given as (g) and (h) on the facing page can actually be proved as on the next two pages [810, 811] to be axiom systems for logic—thus showing that in the end quite remarkable simplification can be achieved relative to ordinary textbook axiom systems.
If one looks at axiom systems of the form {… a, a ∘ b b ∘ a} the first one that one finds that allows only Nand and Nor with 2-value operators is {(a ∘ a) ∘ (a ∘ a) a, a ∘ b b ∘ a}. But as soon as one uses a total of just 6 Nands, one suddenly finds that out of the 3402 possibilities with 3 variables 32 axiom systems equivalent to case (f) above all end up working all the way up to at least 4-value operators. And in fact it then turns out that (f) indeed works as an axiom system for logic.
So what this means is that if one were just to go through a list of the simplest few thousand axiom systems one would already be quite likely to find one that represents logic.
In human intellectual history logic has had great significance. But if one looks just at axiom systems is there anything obviously special about the ones for logic? My guess is that unless one asks about very specific details there is really not—and that standard logic is in a sense distinguished in the end only by its historical context.
One feature of logic is that its axioms effectively describe a single specific operator. But it turns out that there are all sorts of other axioms that also do this. I gave three examples on page 803, and in the picture below I give two more very simple examples. Indeed, given many forms of operator there are always axiom systems that can be found to describe it.
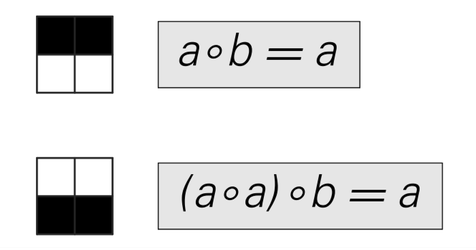
Axiom systems that reproduce equivalence results for the forms of operators shown.



