But if one considers for example analogs of logic for variables with more than two possible values, the picture below shows that one immediately gets systems with still fewer theorems.
So what about proofs? Is there something about these that is somehow special in the case of ordinary logic?
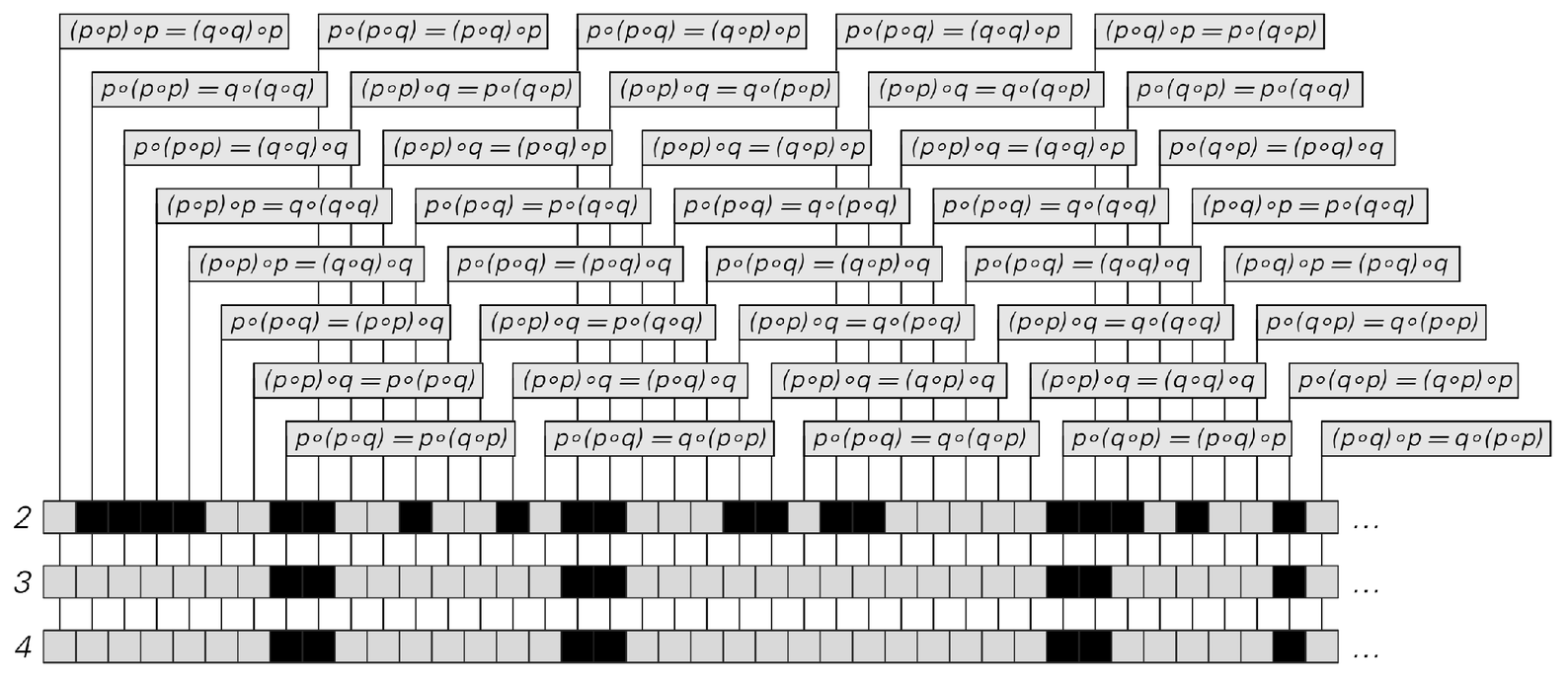
In the axiom systems on page 803 the typical lengths of proofs seem to increase from one system to the next, so that they end up being longest for the last axiom system, which corresponds to logic.
But if one picks a different axiom system for logic—say one of the others on page 808—then the length of a particular proof will usually change. But since one can always just start by proving the new axioms, the change can only be by a fixed amount. And as it turns out, even the simplest axiom system (f) given on page 808 seems to allow fairly short proofs of at least most short theorems.
But as one tries to prove progressively longer theorems it appears that whatever axiom system one uses for logic the lengths of proofs can increase as fast as exponentially. A crucial point, however, is that for theorems of a given length there is always a definite upper limit on the length of proof needed. Yet once again this is not something unique to logic. Indeed, it turns out that this must always be the case for any axiom system—like those on page 803—that ends up allowing essentially only operators of a single form.
So what about other axiom systems?
The very simplest ones on pages 805 and 812 seem to yield proofs that are always comparatively short. But when one looks at axiom systems that are even slightly more complicated the proofs of anything
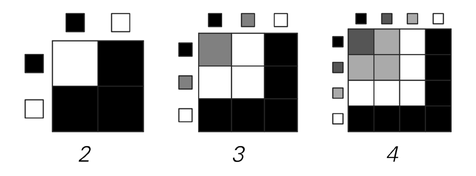 |  |
Theorems in analogs of logic that allow different numbers of truth values. Statements like p ¬ ¬ p do not hold in general with more than 2 truth values.



