It is, however, also possible to consider substitution systems in which elements can simply disappear. If the rate of such disappearances is too large, then almost any pattern will quickly die out. And if there are too few disappearances, then most patterns will grow very rapidly.

But there is always a small fraction of rules in which the creation and destruction of elements is almost perfectly balanced.

The picture below shows one example. The number of elements does end up increasing in this particular example, but only by a fixed amount at each step. And with such slow growth, we can again represent each element by a box of the same size, just as in our original pictures of substitution systems on page 82.

When viewed in this way, however, the pattern produced by the substitution system shown below is seen to have a simple repetitive form. And as it turns out, among substitution systems with the same type of rules, all those which yield slow growth also seem to produce only such simple repetitive patterns.

Knowing this, we might conclude that somehow substitution systems just cannot produce the kind of complexity that we have seen in systems like cellular automata. But as with mobile automata and with Turing machines, we would again be wrong. Indeed, as the pictures on the facing page demonstrate, allowing elements to have three or four colors rather than just two immediately makes much more complicated behavior possible.

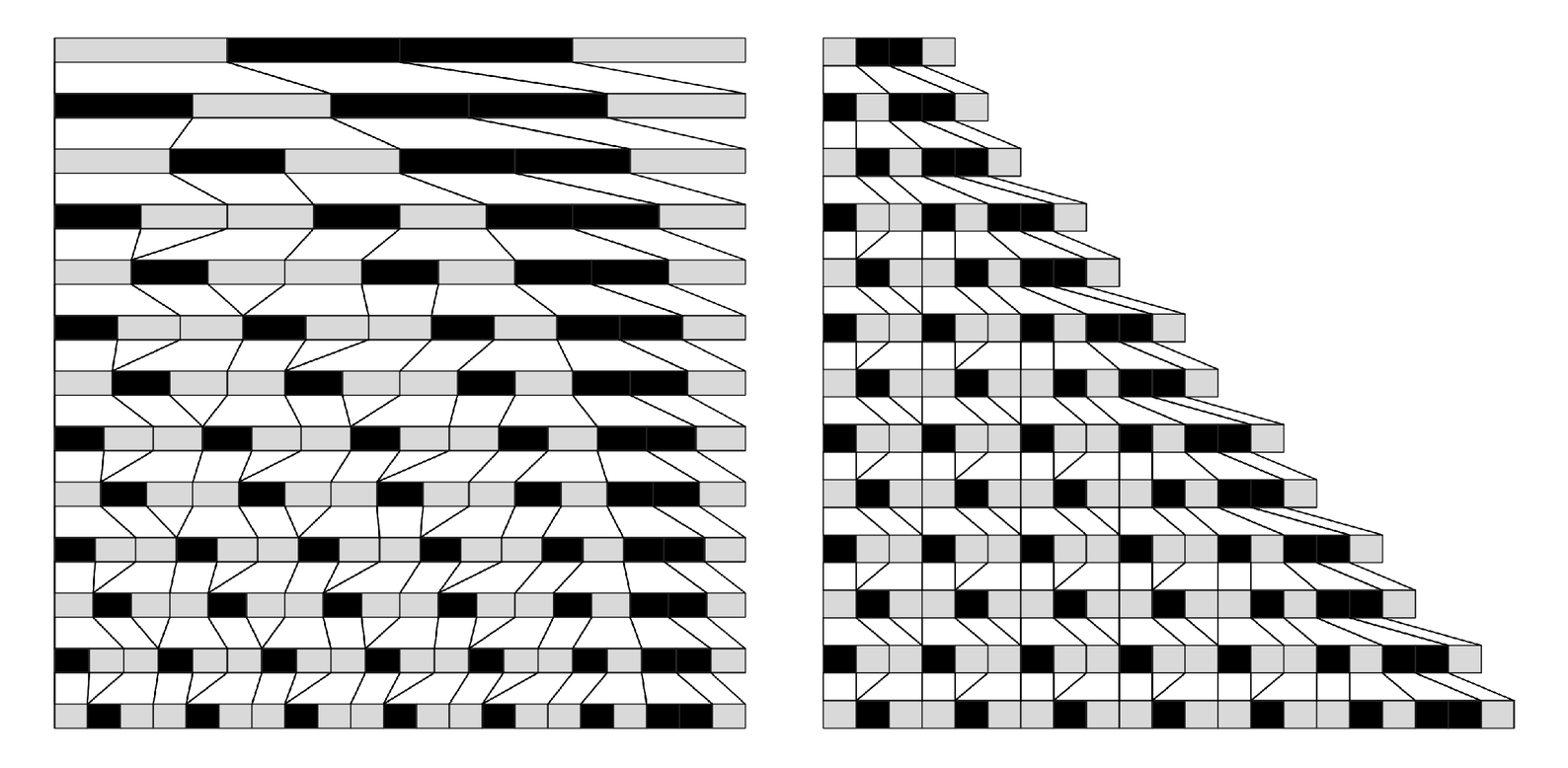
Two views of a substitution system whose rules allow both creation and destruction of elements. In the view on the left, the boxes representing each element are scaled to keep the total width the same, whereas on the right each box has a fixed size, as in our original pictures of substitution systems on page 82. The right-hand view shows that the rates of creation and destruction of elements are balanced closely enough that the total number of elements grows by only a fixed amount at each step.