then it seems that no rule ever gives behavior that is much more complicated than in the picture below.
And from this one might be led to conclude that sequential substitution systems could never produce behavior of any substantial complexity. But having now seen complexity in many other kinds of systems, one might suspect that it should also be possible in sequential substitution systems.
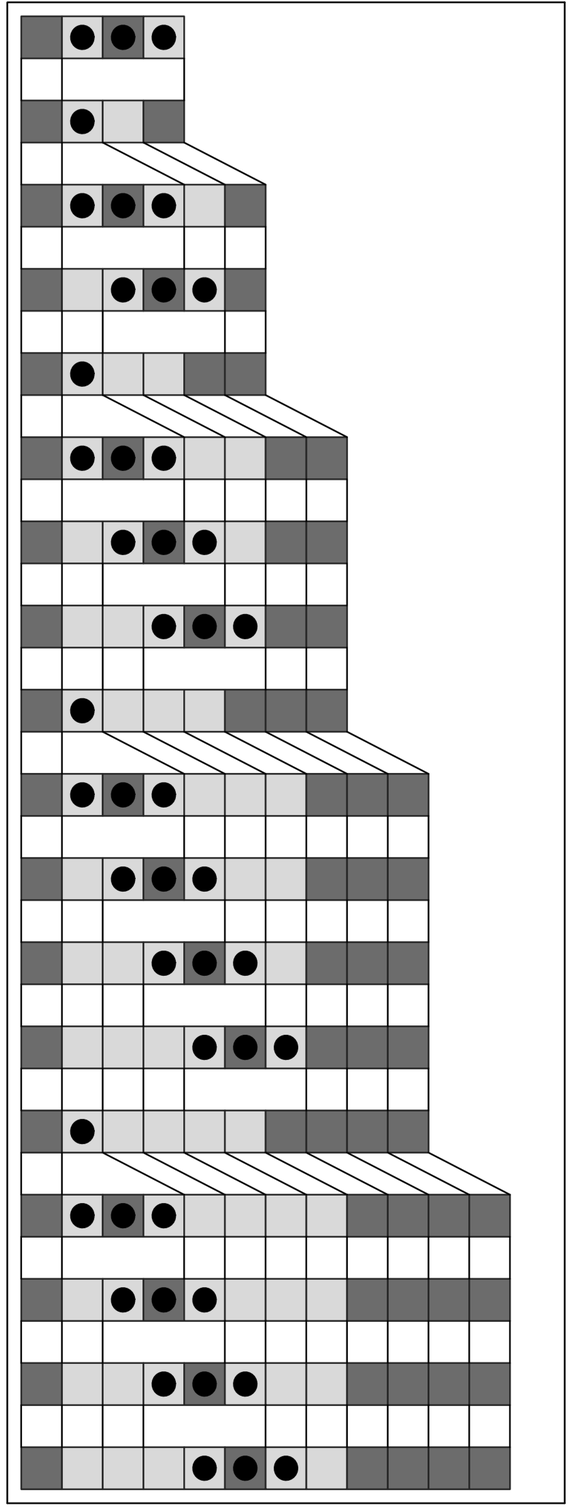
And it turns out that if one allows more than two possible replacements then one can indeed immediately get more complex behavior. The pictures on the facing page show a few examples. In many cases, fairly regular repetitive or nested patterns are still produced.
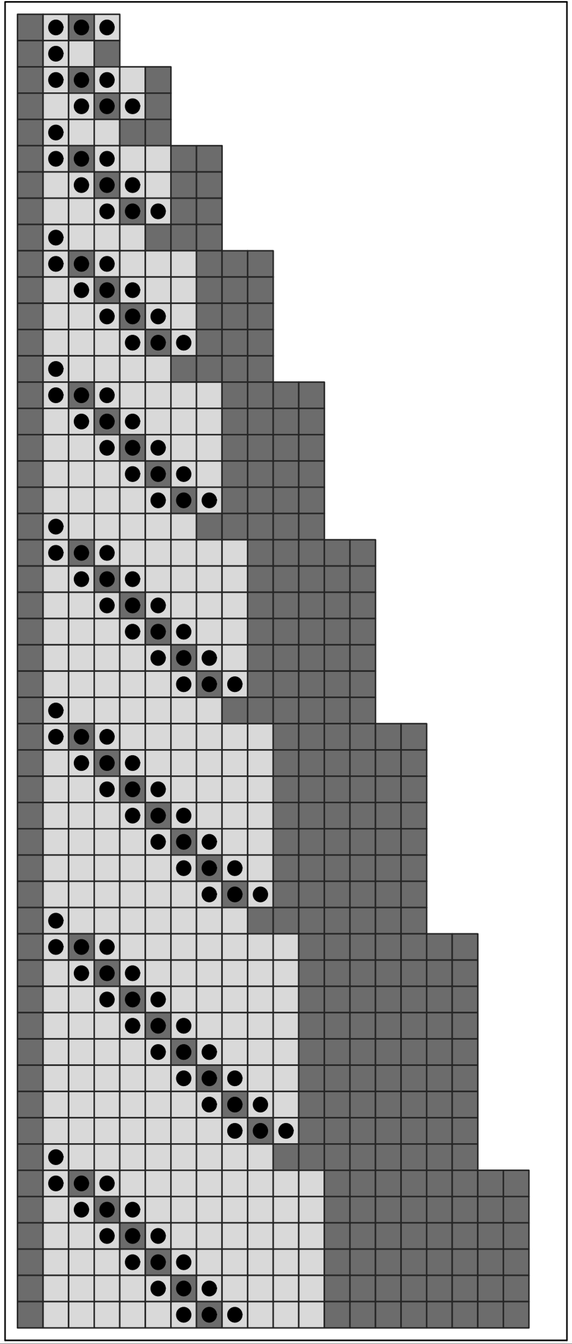
But about once in every 10,000 randomly selected rules, rather different behavior is obtained. Indeed, as the picture on the following page demonstrates, patterns can be produced that seem in many respects random, much like patterns we have seen in cellular automata and other systems.
So this leads to the rather remarkable conclusion that just by using the simple operations available even in a very basic text editor, it is still ultimately possible to produce behavior of great complexity.
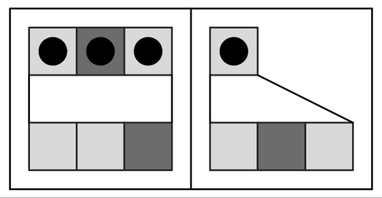 |  |  |
A sequential substitution system whose rule involves two possible replacements. At each step, the whole string is scanned once to try to apply the first replacement, and is then scanned again if necessary to try to apply the second replacement.



