The example just given involves numbers with fractional parts. But it turns out that similar phenomena can also be found in systems that involve only whole numbers.
As a first example, consider a slight variation on the operation of multiplying by 3/2 used in the first picture: if the number at a particular step is even (divisible by 2), then simply multiply that number by 3/2, getting a whole number as the result. But if the number is odd, then first add 1—so as to get an even number—and only then multiply by 3/2.

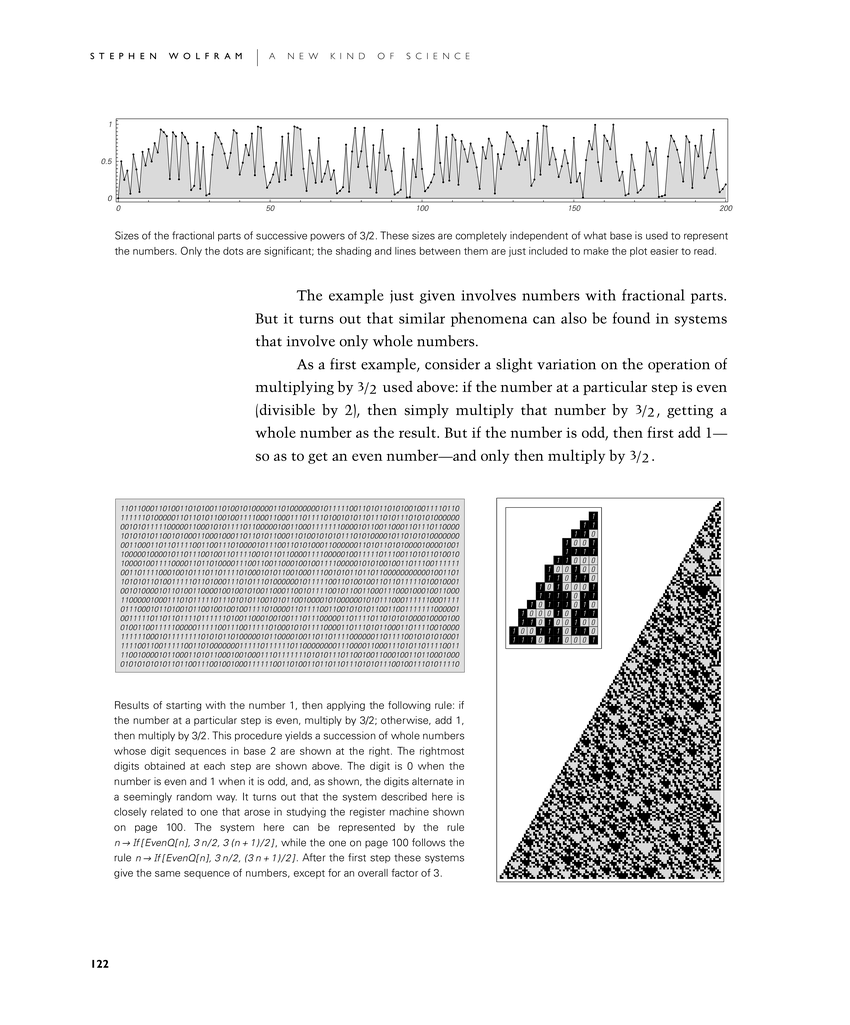
Sizes of the fractional parts of successive powers of 3/2. These sizes are completely independent of what base is used to represent the numbers. Only the dots are significant; the shading and lines between them are just included to make the plot easier to read.
 | 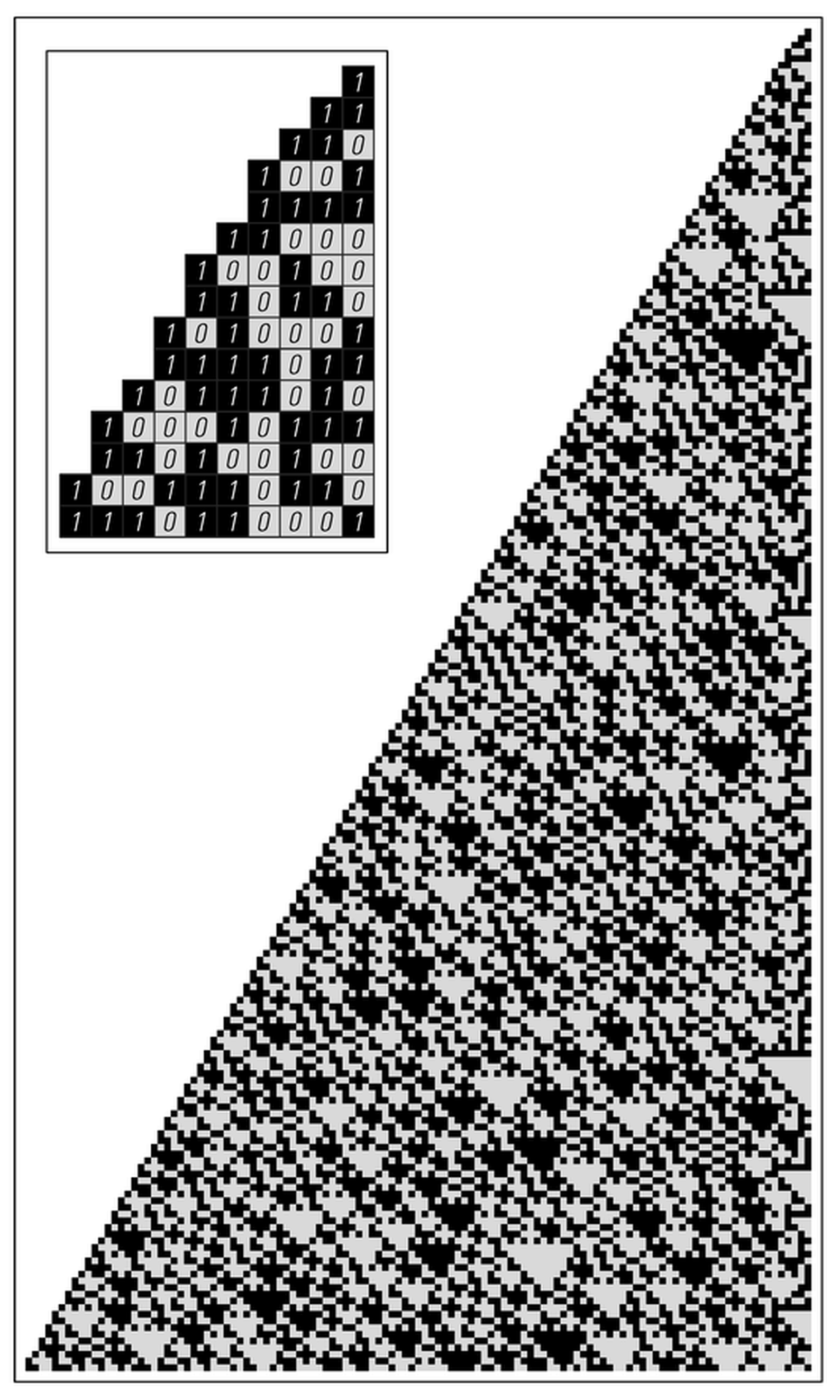 |
Results of starting with the number 1, then applying the following rule: if the number at a particular step is even, multiply by 3/2; otherwise, add 1, then multiply by 3/2. This procedure yields a succession of whole numbers whose digit sequences in base 2 are shown at the right. The rightmost digits obtained at each step are shown on the left. The digit is 0 when the number is even and 1 when it is odd, and, as shown, the digits alternate in a seemingly random way. It turns out that the system described here is closely related to one that arose in studying the register machine shown on page 100. The system here can be represented by the rule n If[EvenQ[n], 3n/2, 3(n + 1)/2], while the one on page 100 follows the rule n If[EvenQ[n], 3n/2, (3n + 1)/2]. After the first step these systems give the same sequence of numbers, except for an overall factor of 3.