This procedure is always guaranteed to give a whole number. And starting with 1, the sequence of numbers one gets is 1, 3, 6, 9, 15, 24, 36, 54, 81, 123, 186, 279, 420, 630, 945, 1419, 2130, 3195, 4794, ...
Some of these numbers are even, while some are odd. But as the results at the bottom of the facing page illustrate, the sequence of which numbers are even and which are odd seems to be completely random.
Despite this randomness, however, the overall sizes of the numbers obtained still grow in a rather regular way. But by changing the procedure just slightly, one can get much less regular growth.
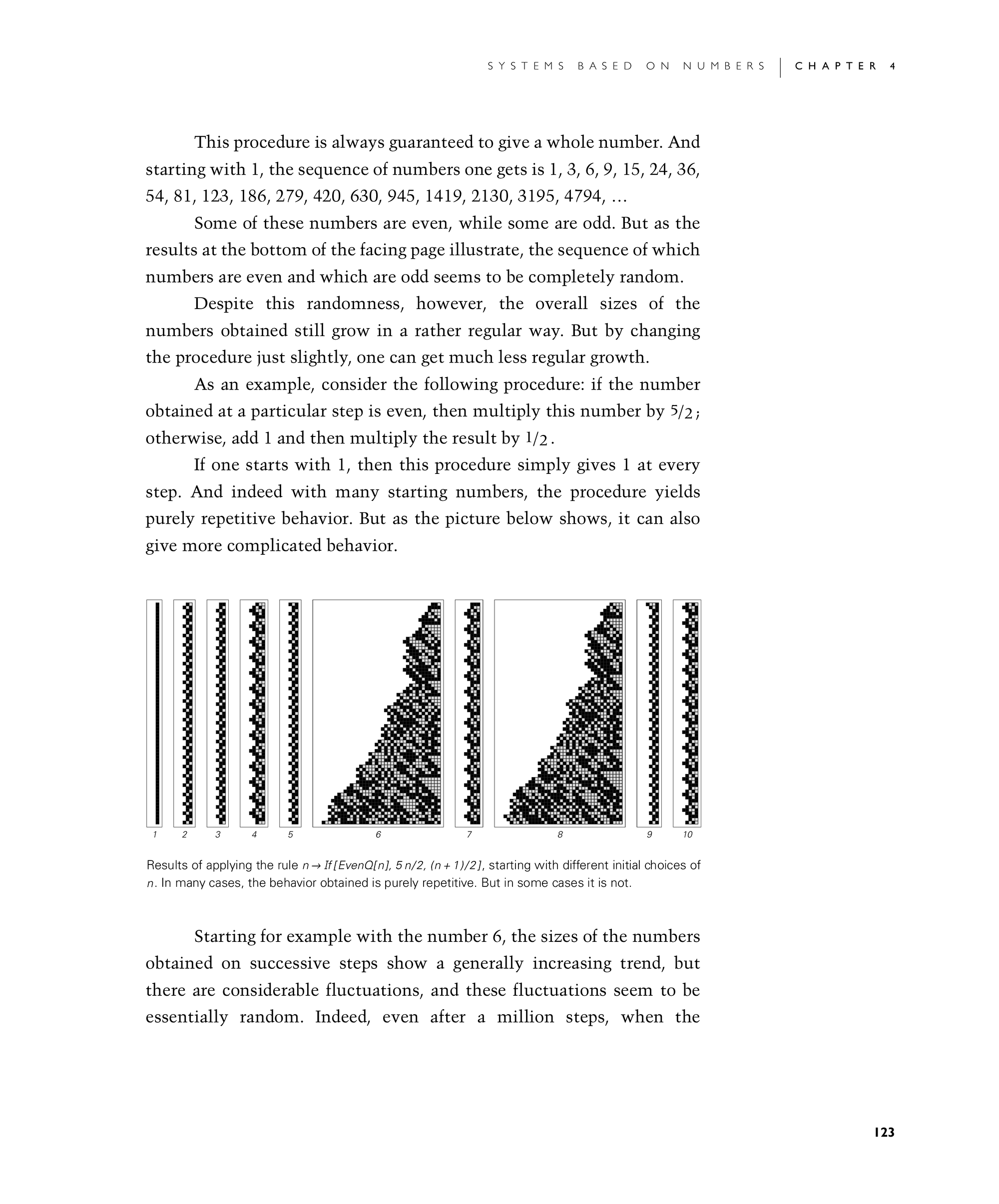
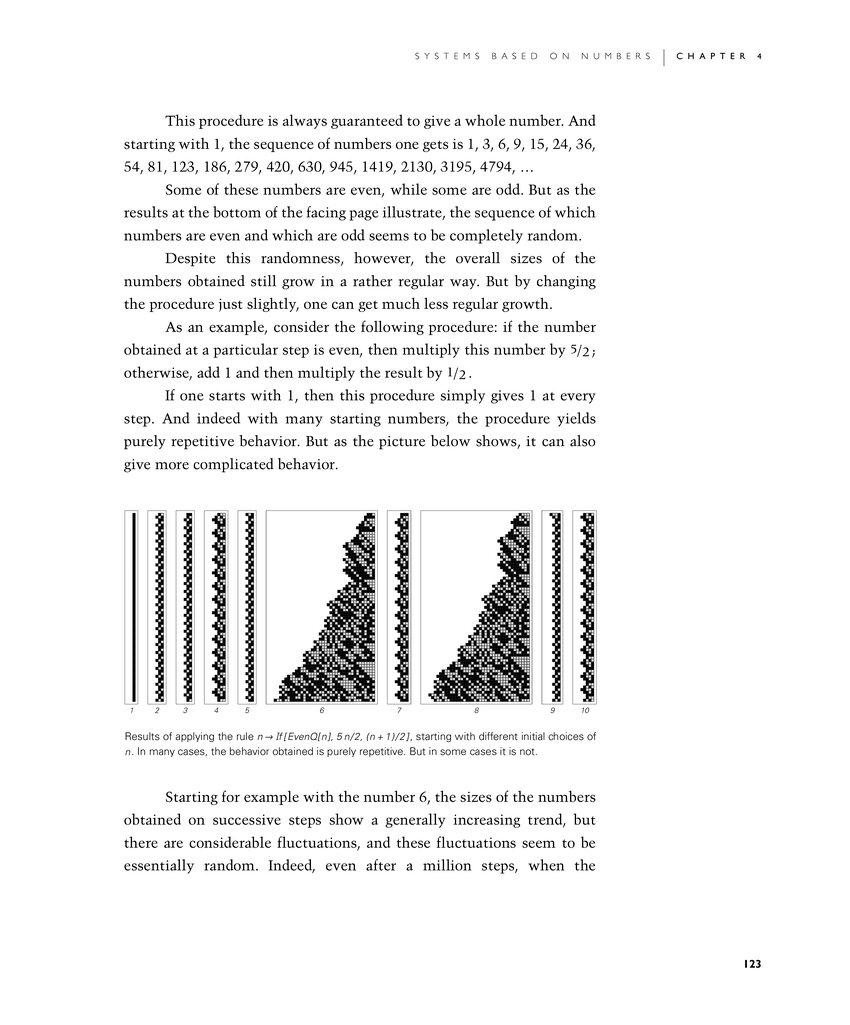
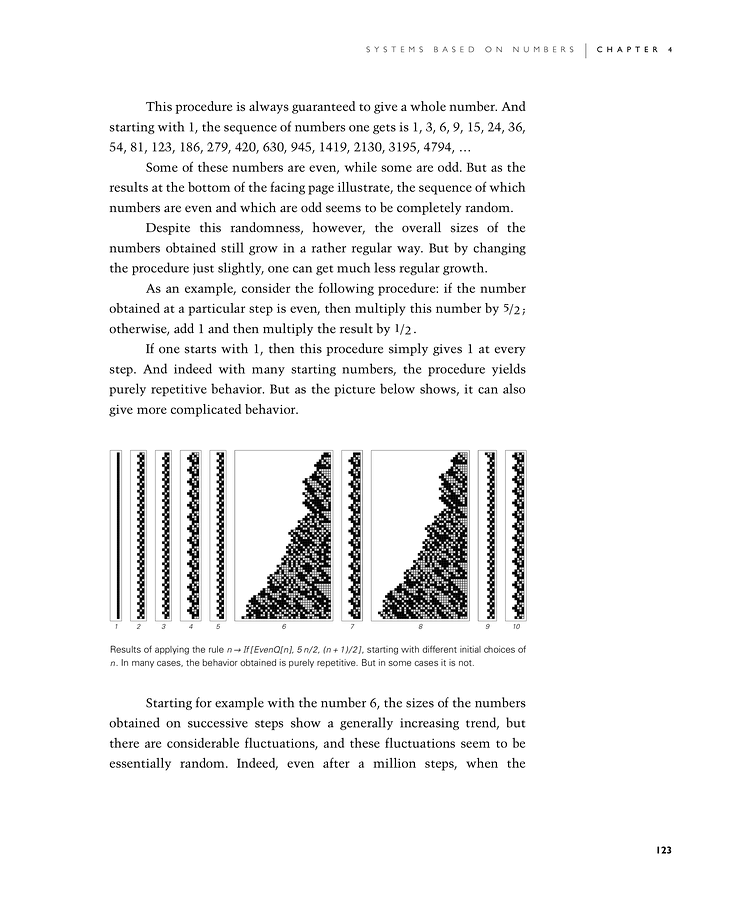
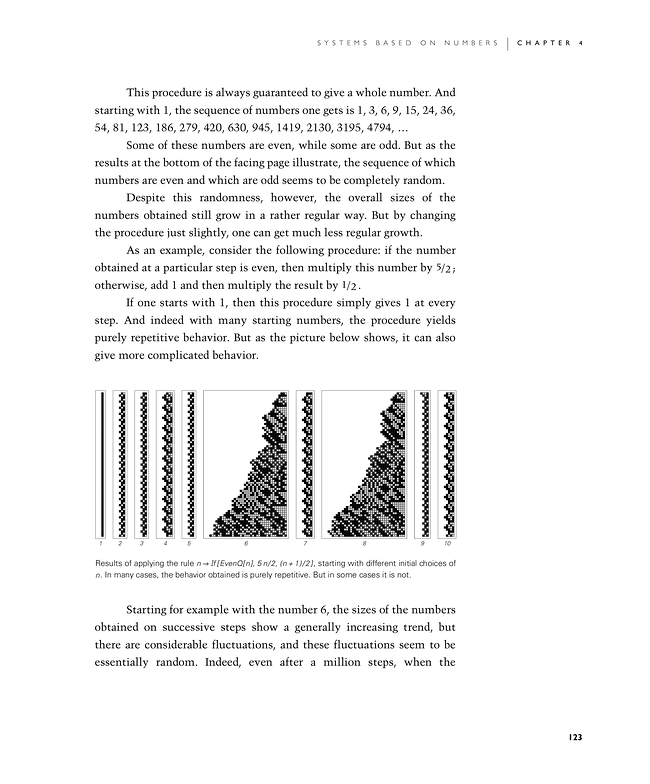
As an example, consider the following procedure: if the number obtained at a particular step is even, then multiply this number by 5/2; otherwise, add 1 and then multiply the result by 1/2.
If one starts with 1, then this procedure simply gives 1 at every step. And indeed with many starting numbers, the procedure yields purely repetitive behavior. But as the picture below shows, it can also give more complicated behavior.
Starting for example with the number 6, the sizes of the numbers obtained on successive steps show a generally increasing trend, but there are considerable fluctuations, and these fluctuations seem to be essentially random. Indeed, even after a million steps, when the
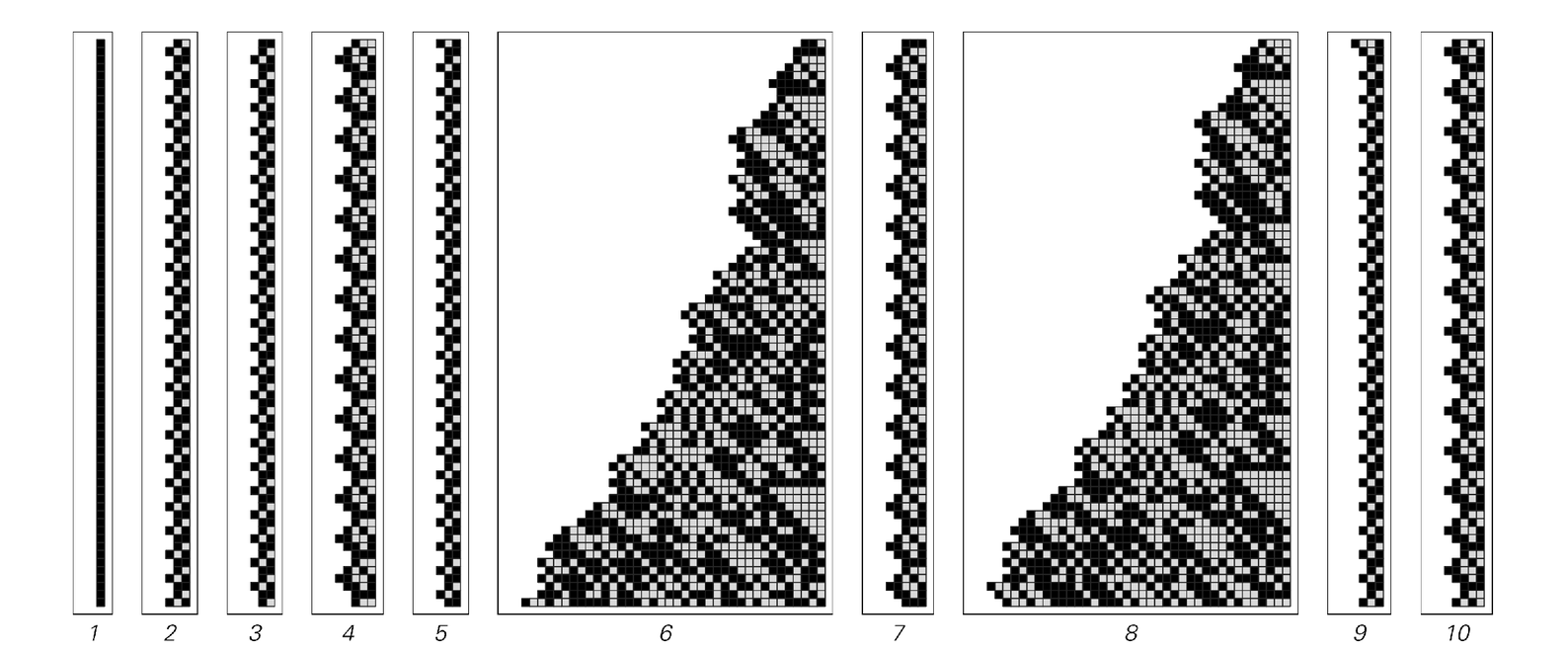
Results of applying the rule n If[EvenQ[n], 5n/2, (n + 1)/2], starting with different initial choices of n. In many cases, the behavior obtained is purely repetitive. But in some cases it is not.