in the top picture below. With two nodes, there are already three possible patterns of connections, as shown on the second line below. And as the number of nodes increases, the number of possible different networks grows very rapidly.
For most of these networks there is no way of laying out their nodes so as to get a picture that looks like anything much more than a random jumble of wires. But it is nevertheless possible to construct many specific networks that have easily recognizable forms, as shown in the pictures on the facing page.
Each of the networks illustrated at the top of the facing page consists at the lowest level of a collection of identical nodes. But the remarkable fact that we see is that just by changing the pattern of
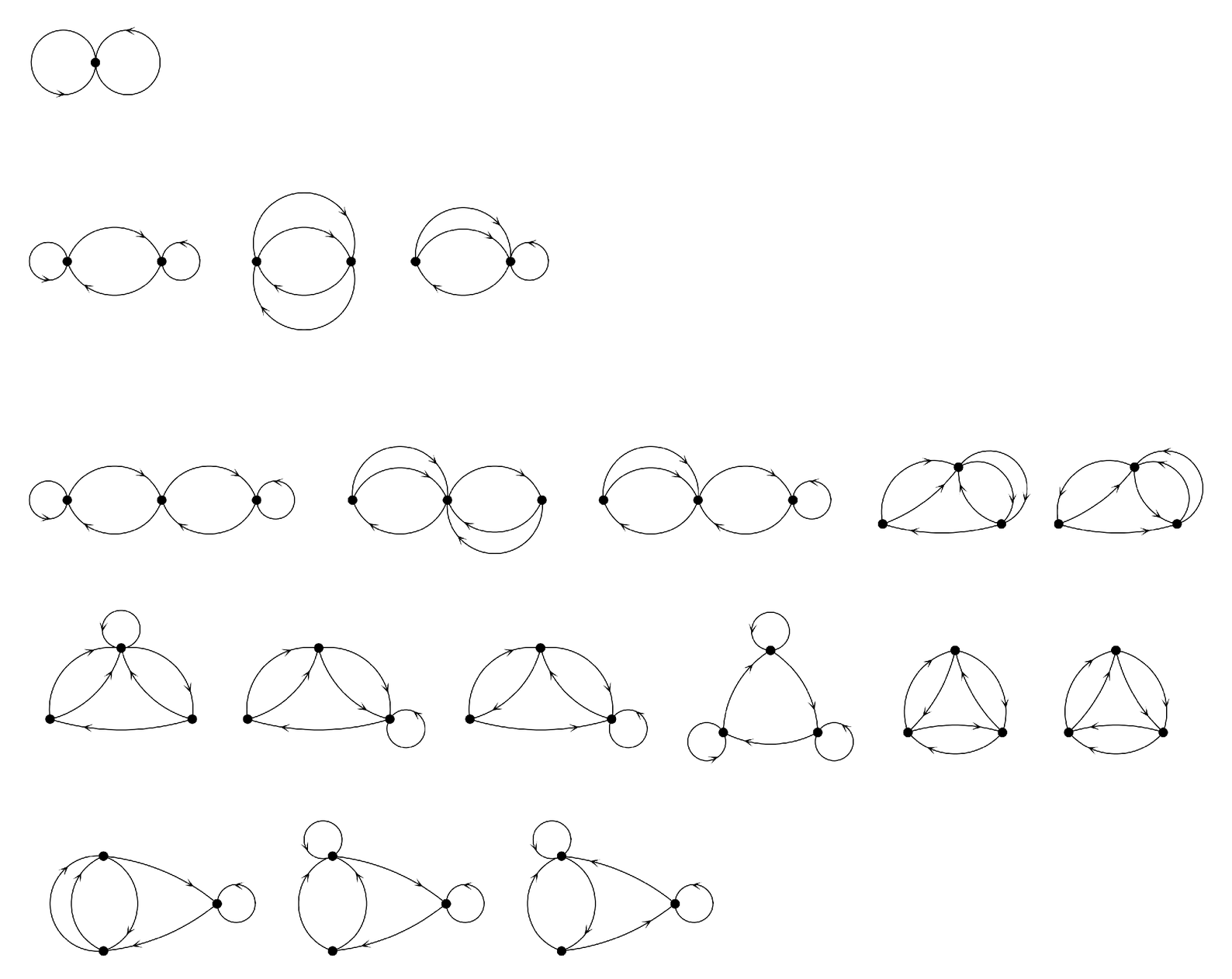
Possible networks formed by having one, two or three nodes, with two connections coming out of each node. The picture shows all inequivalent cases ignoring labels, but excludes networks in which there are nodes which cannot be reached by connections from other nodes.



