connections between these nodes it is possible to get structures that effectively correspond to arrays with different numbers of dimensions.

Example (a) shows a network that is effectively one-dimensional. The network consists of pairs of nodes that can be arranged in a sequence in which each pair is connected to one other pair on the left and another pair on the right.

But there is nothing intrinsically one-dimensional about the structure of network systems. And as example (b) demonstrates, it is just a matter of rearranging connections to get a network that looks like a two-dimensional rather than a one-dimensional array. Each individual node in example (b) still has exactly two connections coming out of it, but now the overall pattern of connections is such that every block of nodes is connected to four rather than two neighboring blocks, so that the network effectively forms a two-dimensional square grid.

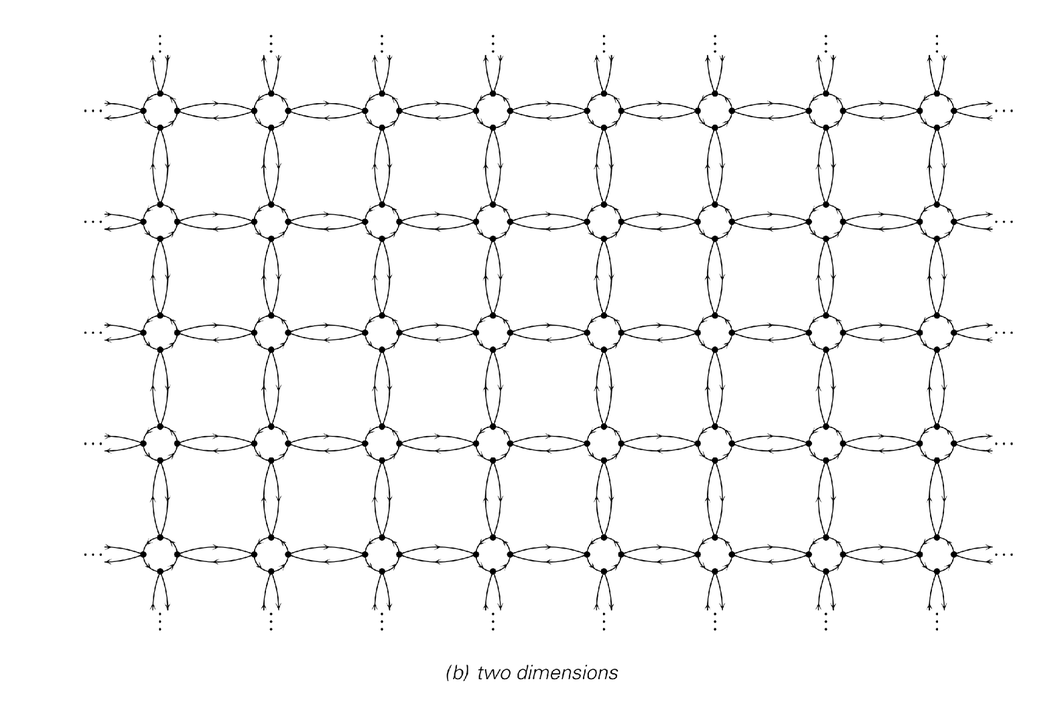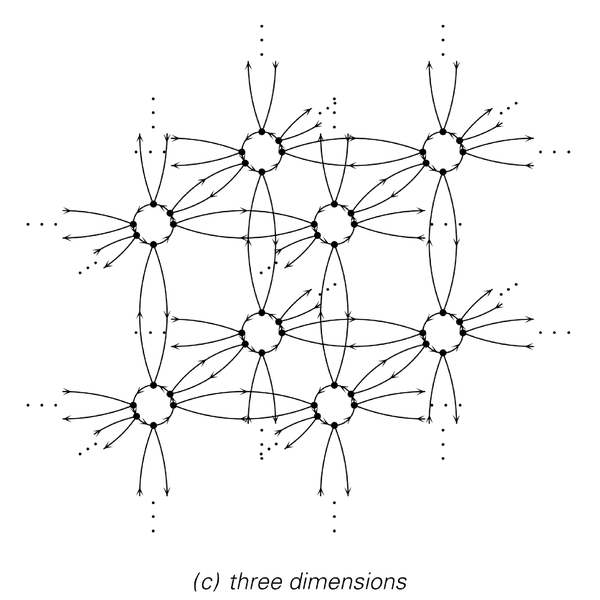Examples of networks that correspond to arrays in one, two and three dimensions. At an underlying level, each network consists just of a collection of nodes with two connections coming from each node. But by setting up appropriate patterns for these connections, one can get networks with very different effective geometrical structures.