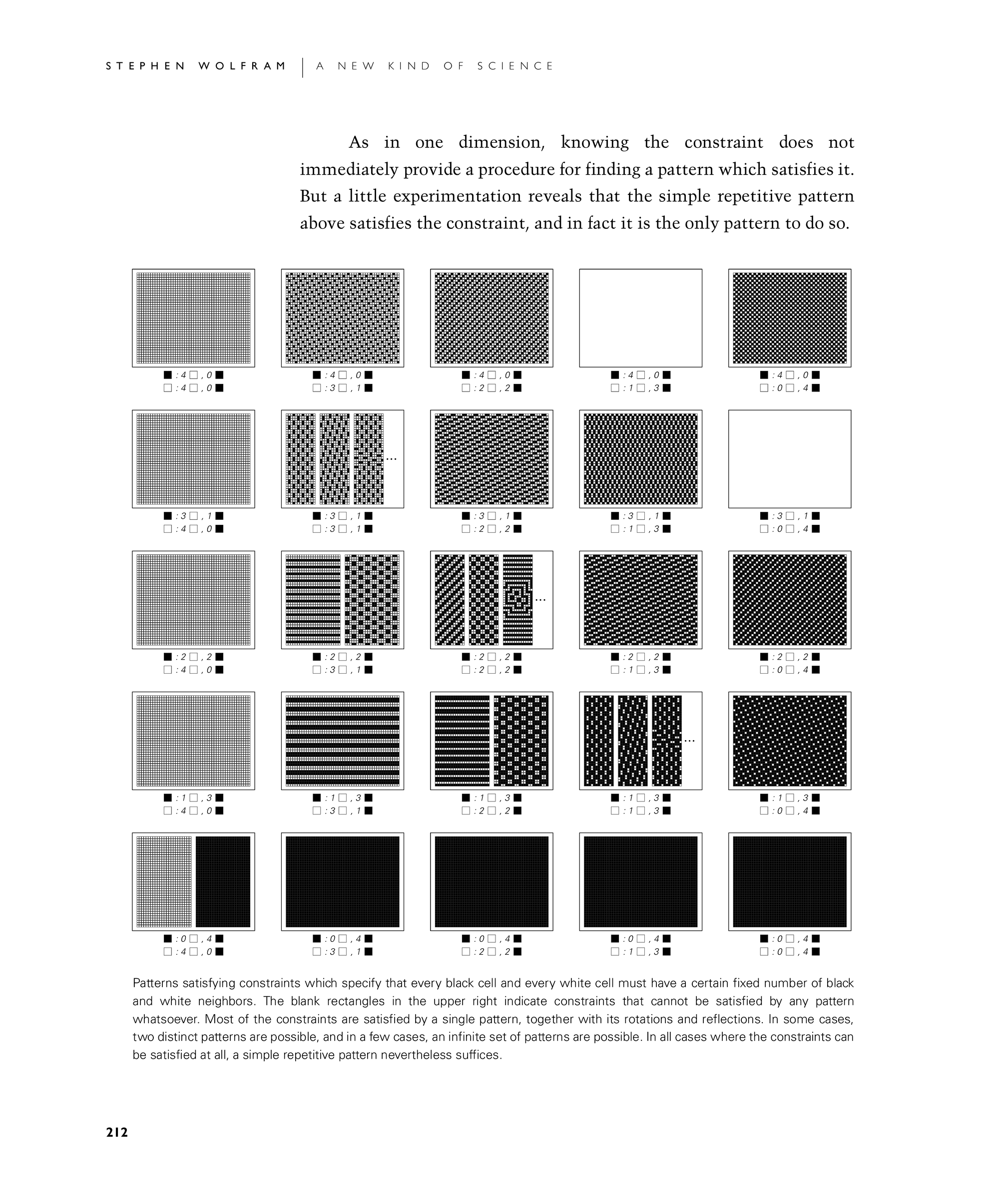
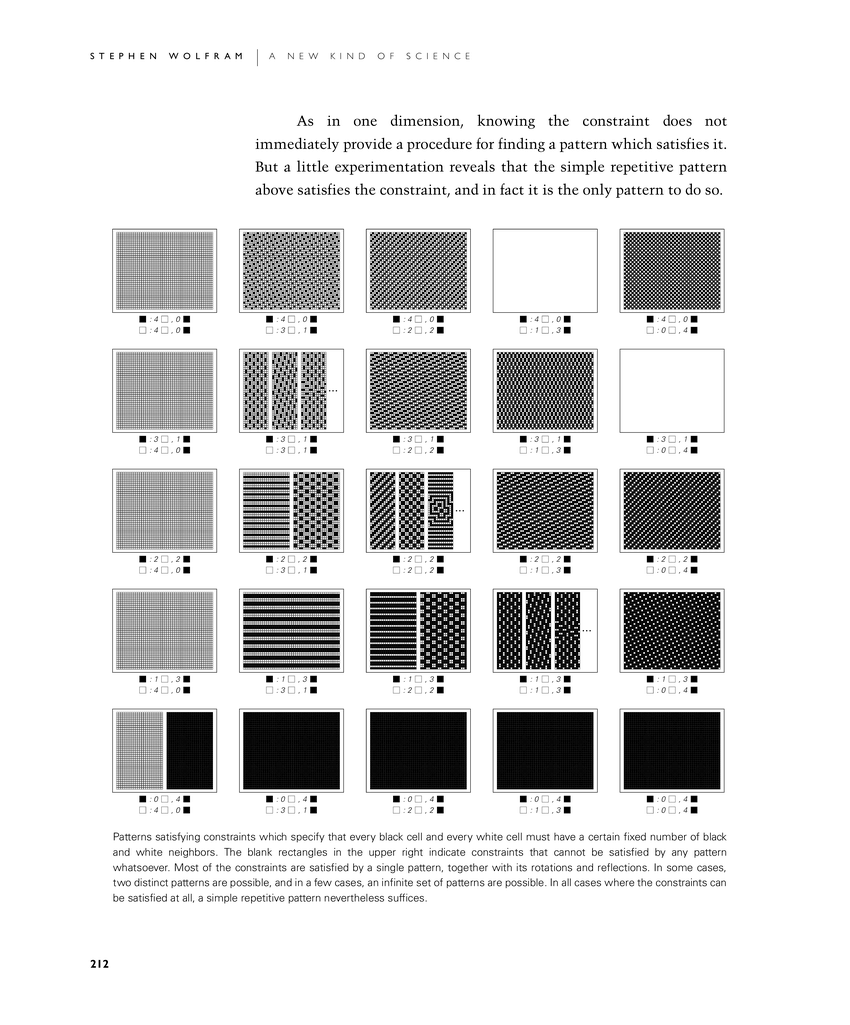
As in one dimension, knowing the constraint does not immediately provide a procedure for finding a pattern which satisfies it. But a little experimentation reveals that the simple repetitive pattern above satisfies the constraint, and in fact it is the only pattern to do so.

Patterns satisfying constraints which specify that every black cell and every white cell must have a certain fixed number of black and white neighbors. The blank rectangles in the upper right indicate constraints that cannot be satisfied by any pattern whatsoever. Most of the constraints are satisfied by a single pattern, together with its rotations and reflections. In some cases, two distinct patterns are possible, and in a few cases, an infinite set of patterns are possible. In all cases where the constraints can be satisfied at all, a simple repetitive pattern nevertheless suffices.