What about other constraints? The pictures on the facing page show schematically what happens with constraints that require each cell to have various numbers of black and white neighbors.
Several kinds of results are seen. In the two cases shown as blank rectangles on the upper right, there are no patterns at all that satisfy the constraints. But in every other case the constraints can be satisfied, though typically by just one or sometimes two simple infinite repetitive patterns. In the three cases shown in the center a whole range of mixtures of different repetitive patterns are possible. But ultimately, in every case where some pattern can work, a simple repetitive pattern is all that is needed.
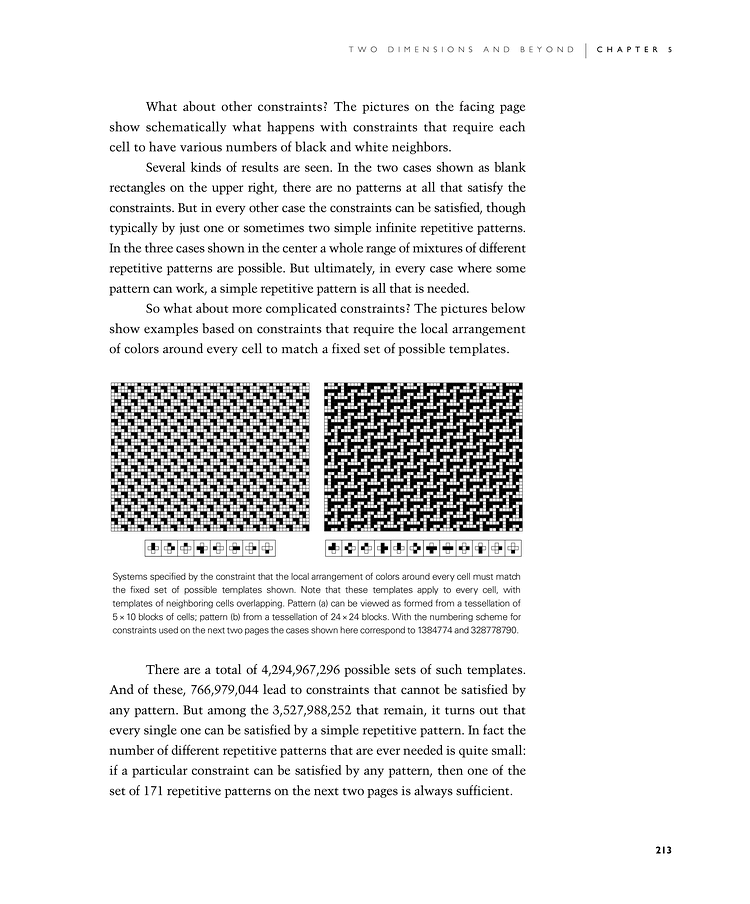
So what about more complicated constraints? The pictures below show examples based on constraints that require the local arrangement of colors around every cell to match a fixed set of possible templates.
There are a total of 4,294,967,296 possible sets of such templates. And of these, 766,979,044 lead to constraints that cannot be satisfied by any pattern. But among the 3,527,988,252 that remain, it turns out that every single one can be satisfied by a simple repetitive pattern. In fact the number of different repetitive patterns that are ever needed is quite small: if a particular constraint can be satisfied by any pattern, then one of the set of 171 repetitive patterns on the next two pages [214, 215] is always sufficient.

Systems specified by the constraint that the local arrangement of colors around every cell must match the fixed set of possible templates shown. Note that these templates apply to every cell, with templates of neighboring cells overlapping. Pattern (a) can be viewed as formed from a tessellation of 5×10 blocks of cells; pattern (b) from a tessellation of 24×24 blocks. With the numbering scheme for constraints used on the next two pages [214, 215] the cases shown here correspond to 1384774 and 328778790.