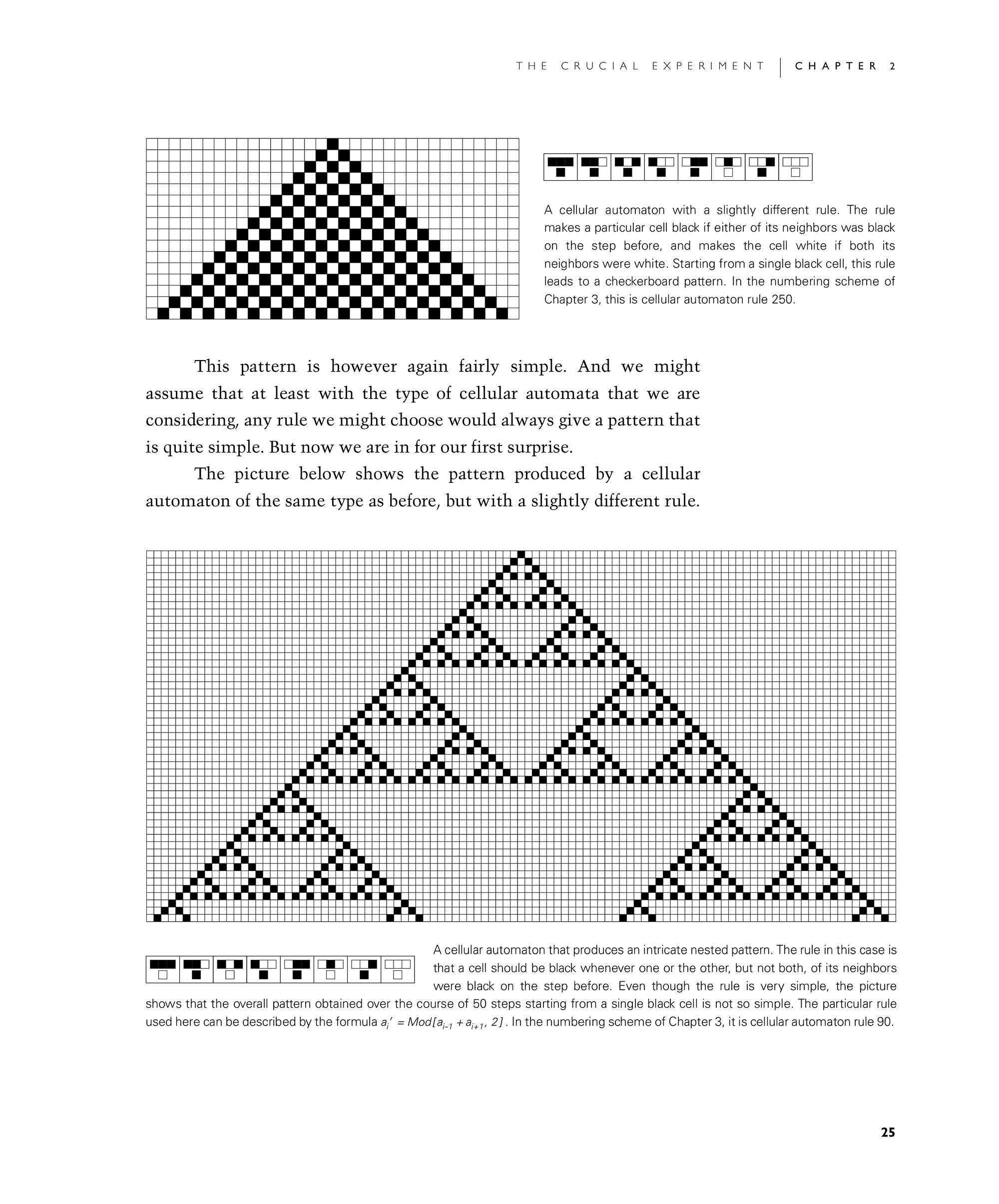
This pattern is however again fairly simple. And we might assume that at least with the type of cellular automata that we are considering, any rule we might choose would always give a pattern that is quite simple. But now we are in for our first surprise.
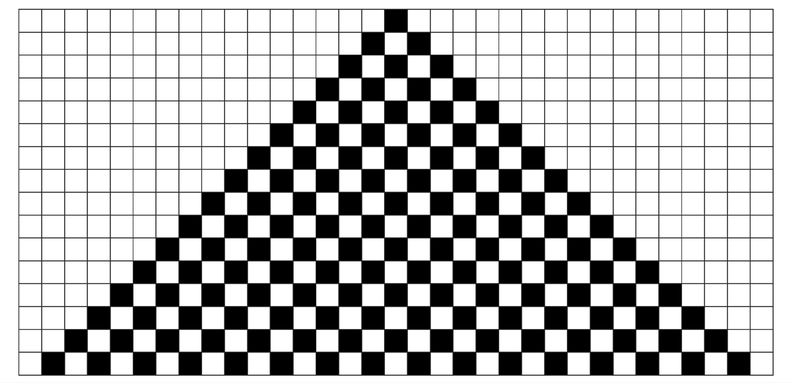
The bottom picture shows the pattern produced by a cellular automaton of the same type as before, but with a slightly different rule.
 |  |
A cellular automaton with a slightly different rule. The rule makes a particular cell black if either of its neighbors was black on the step before, and makes the cell white if both its neighbors were white. Starting from a single black cell, this rule leads to a checkerboard pattern. In the numbering scheme of Chapter 3, this is cellular automaton rule 250.

A cellular automaton that produces an intricate nested pattern. The rule in this case is that a cell should be black whenever one or the other, but not both, of its neighbors were black on the step before. Even though the rule is very simple, the picture shows that the overall pattern obtained over the course of 50 steps starting from a single black cell is not so simple. The particular rule used here can be described by the formula ai'= Mod[ai-1 + ai+1, 2]. In the numbering scheme of Chapter 3, it is cellular automaton rule 90.