random, then progressively modifies the pattern so as to make it closer to satisfying the constraints.

As a specific example consider taking a series of steps, and at each step picking a square in the array discussed above at random, then reversing the color of this square whenever doing so will not increase the total number of squares in the array that violate the constraints.

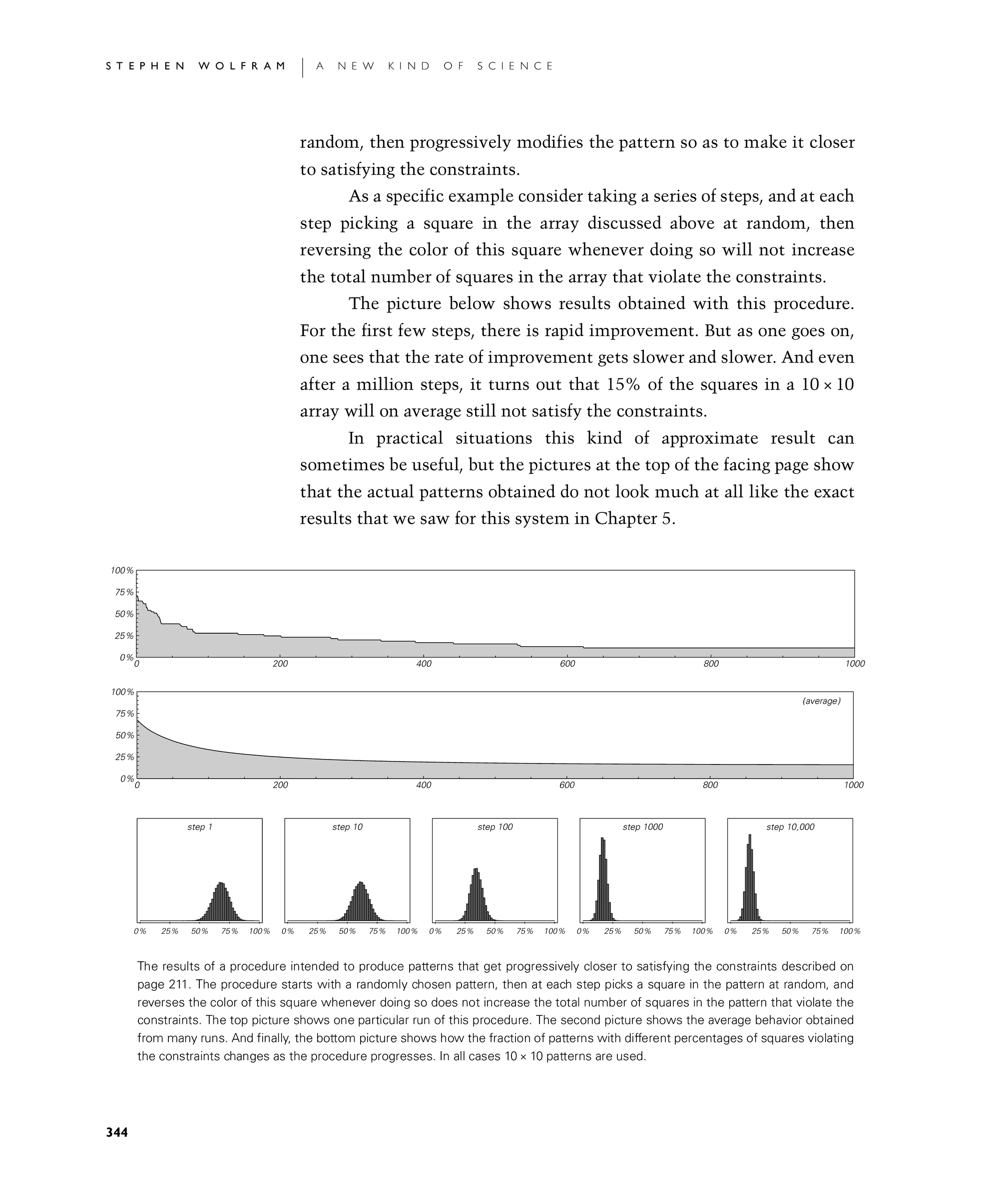
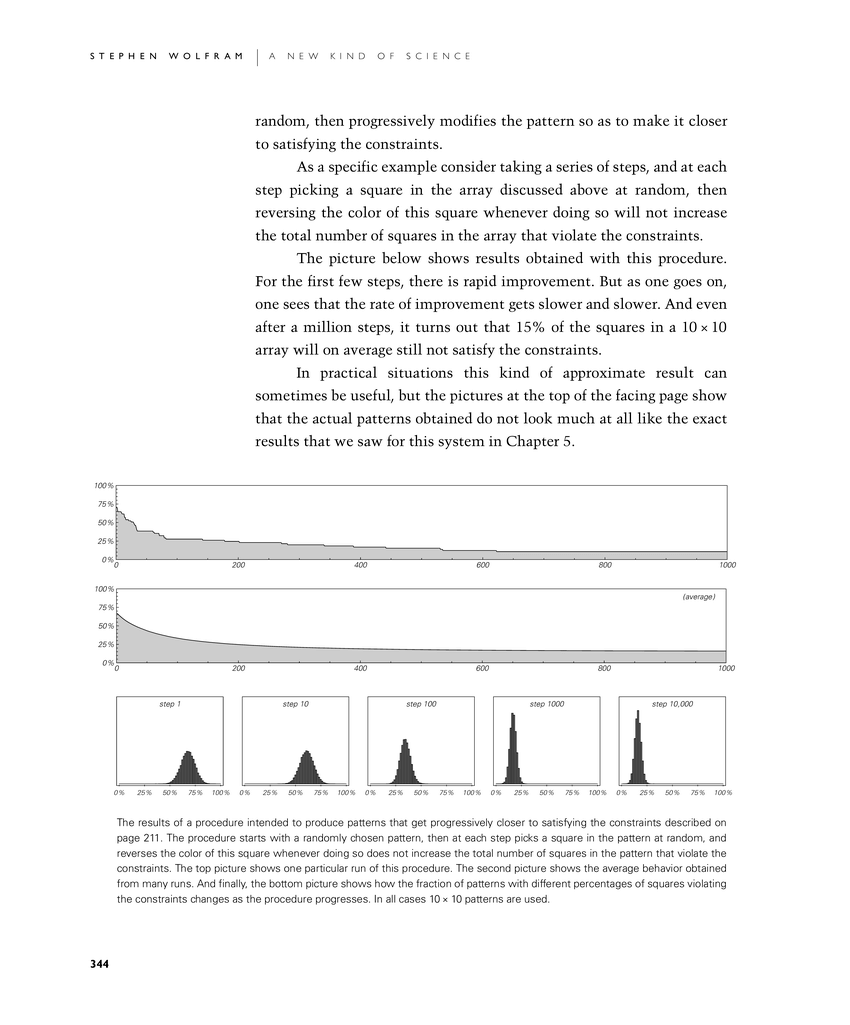
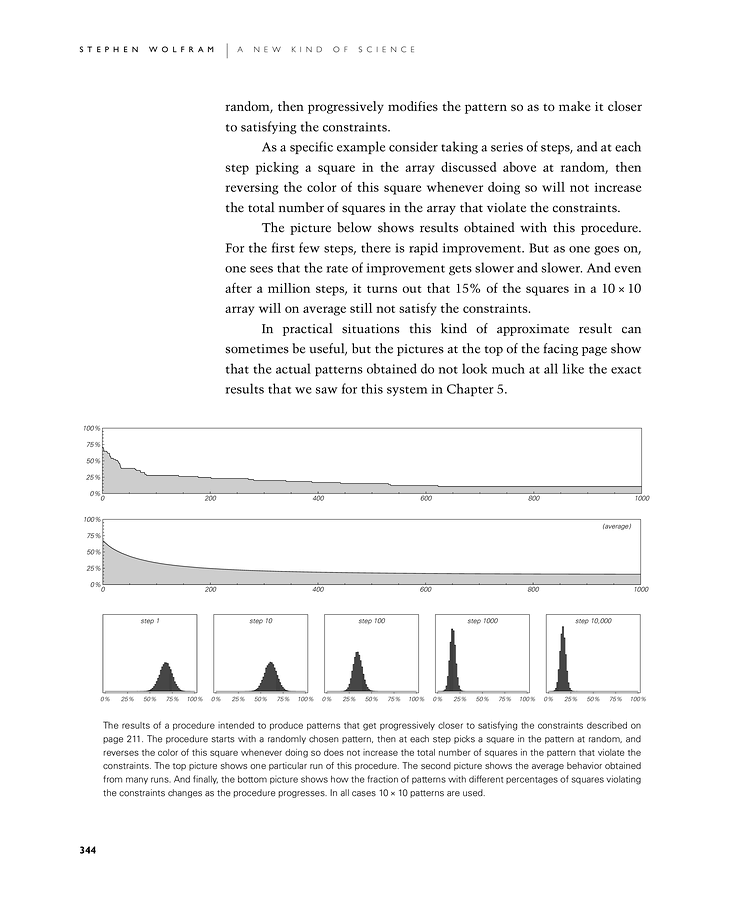
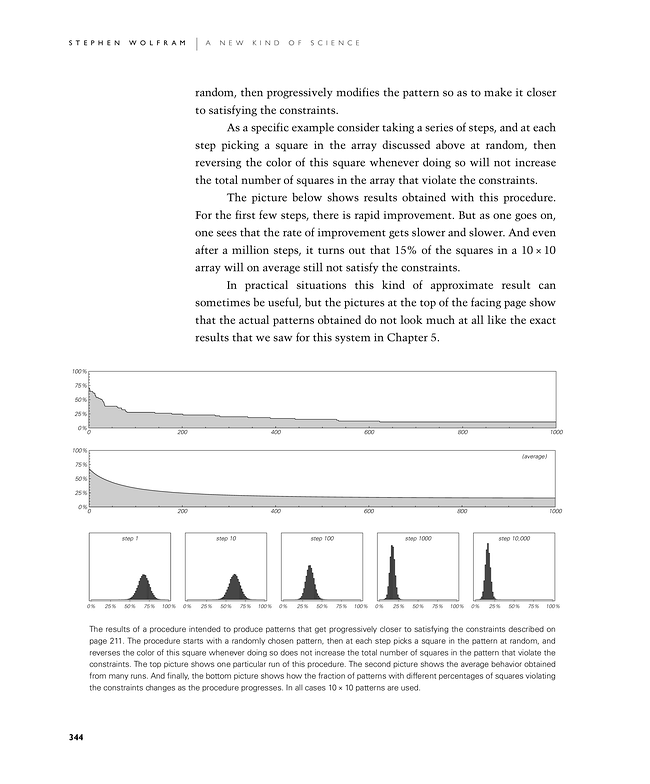
The picture below shows results obtained with this procedure. For the first few steps, there is rapid improvement. But as one goes on, one sees that the rate of improvement gets slower and slower. And even after a million steps, it turns out that 15% of the squares in a 10×10 array will on average still not satisfy the constraints.

In practical situations this kind of approximate result can sometimes be useful, but the pictures at the top of the facing page show that the actual patterns obtained do not look much at all like the exact results that we saw for this system in Chapter 5.