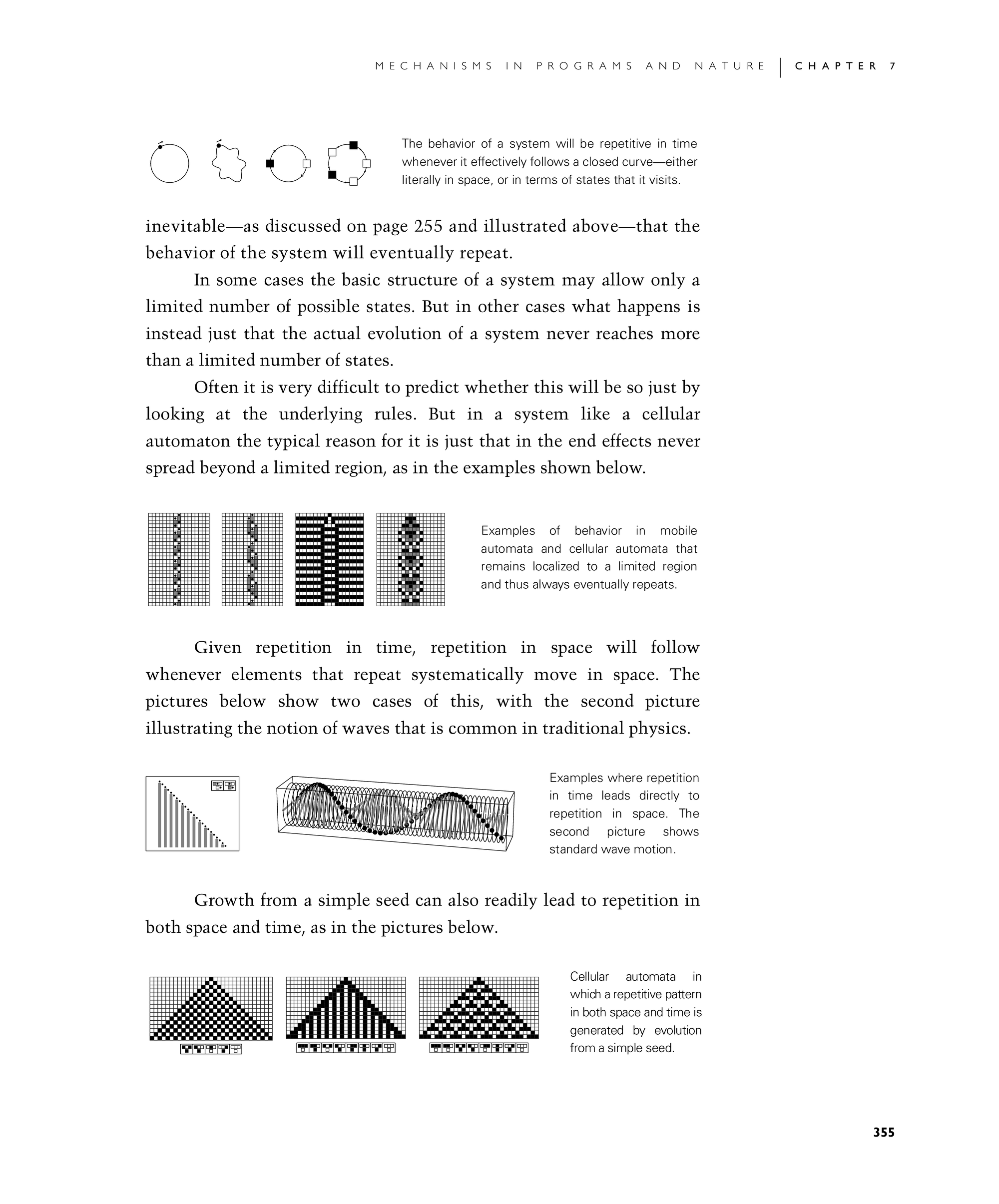
inevitable—as discussed on page 255 and illustrated in the first set of pictures below—that the behavior of the system will eventually repeat.

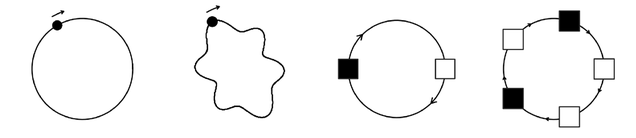
In some cases the basic structure of a system may allow only a limited number of possible states. But in other cases what happens is instead just that the actual evolution of a system never reaches more than a limited number of states.

Often it is very difficult to predict whether this will be so just by looking at the underlying rules. But in a system like a cellular automaton the typical reason for it is just that in the end effects never spread beyond a limited region, as in the examples shown in the first set of pictures below.

Given repetition in time, repetition in space will follow whenever elements that repeat systematically move in space. The pictures below show two cases of this, with the second picture illustrating the notion of waves that is common in traditional physics.

Growth from a simple seed can also readily lead to repetition in both space and time, as in the second set of pictures below.

The behavior of a system will be repetitive in time whenever it effectively follows a closed curve—either literally in space, or in terms of states that it visits.

Examples of behavior in mobile automata and cellular automata that remains localized to a limited region and thus always eventually repeats.

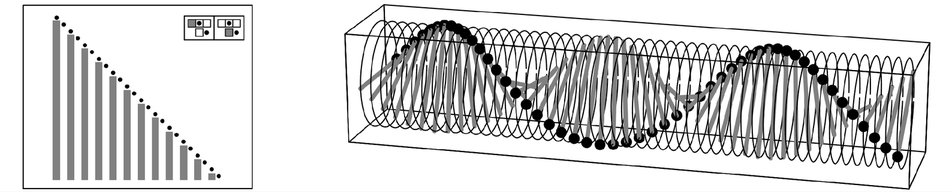
Examples where repetition in time leads directly to repetition in space. The second picture shows standard wave motion.

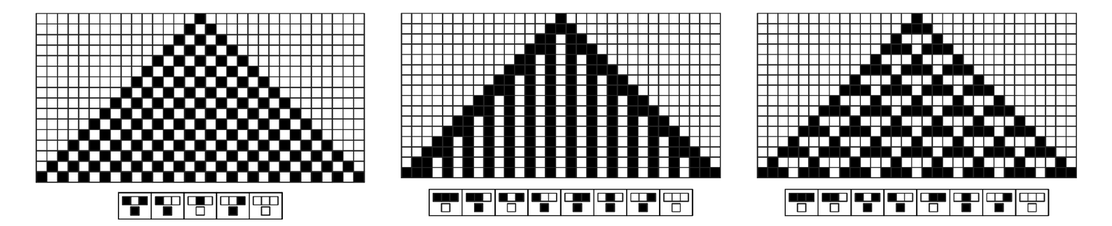
Cellular automata in which a repetitive pattern in both space and time is generated by evolution from a simple seed.