And with this setup, if the underlying rules replace each block by one that contains the same number of black cells, it is inevitable that the system as a whole will conserve the total number of black cells.

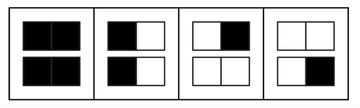
With two possible colors and blocks of size two the only kinds of block cellular automata that conserve the total number of black cells are the ones shown in the second set of pictures—and all of these exhibit rather trivial behavior.

An example of a block cellular automaton. The system works by partitioning the sequence of cells that exists at each step into pairs, then replacing these pairs by other pairs according to the rule shown. The choice of whether to pair a cell with its left or right neighbor alternates on successive steps. Like many block cellular automata, the system shown is reversible, since in the rule each pair has a unique predecessor. It does not, however, conserve the total number of black cells.

Block cellular automata with two possible colors and blocks of size two that conserve the total number of black cells (the last example has this property only on alternate steps). It so happens that all but the second of the rules shown here not only conserve the total number of black cells but also turn out to be reversible.