fundamentally larger range if one allowed, say, four or five connections rather than just three. But in fact one cannot, since any node with more than three connections can in effect always be broken into a collection of nodes with exactly three connections, as in the first set of pictures below.
So what this means is that it is in a sense always sufficient to consider networks with exactly three connections at each node. And it is therefore these networks that I will use here in discussing fundamental models of space.
The second set of pictures below show a few small examples of such networks. And already considerable diversity is evident. But none of the networks shown seem to have many properties familiar from ordinary space.
So how then can one get networks that correspond to ordinary space? The first step is to consider networks that have much larger numbers of nodes. And as examples of these, the pictures at the top of the facing page show networks that are specifically constructed to correspond to ordinary one-, two- and three-dimensional space.
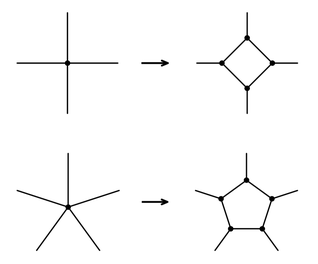
Examples of how nodes with more than three connections can be decomposed into collections of nodes with exactly three connections.
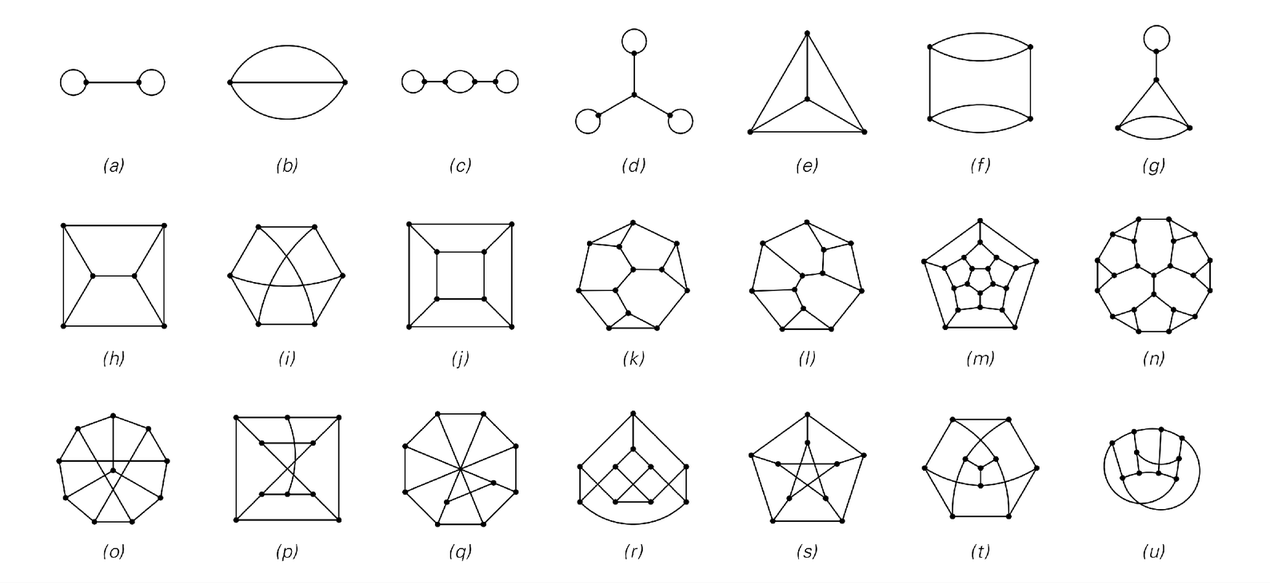
Examples of small networks with exactly three connections at each node. The first line shows all possible networks with up to four nodes. In what follows I consider only non-degenerate networks, in which there is at most one connection between any two nodes. Example (i) is the smallest network that cannot be drawn in two dimensions without lines crossing. Examples (k) and (l) are the smallest networks that have no symmetries between different nodes. Example (e) corresponds to the net of a tetrahedron, (j) to the net of a cube, and (m) to the net of a dodecahedron. Examples (o) through (u) show seven ways of drawing the same network, in this case the so-called Petersen network.



