Each of these networks is at the lowest level just a collection of nodes with certain connections. But the point is that the overall pattern of these connections is such that on a large scale there emerges a clear correspondence to ordinary space of a particular dimension.

The first set of pictures below are drawn so as to make this correspondence obvious. But what if one was just presented with the raw pattern of connections for some network? How could one see whether the network could correspond to ordinary space of a particular dimension?

The second set of pictures below illustrate the main difficulty: given only its pattern of connections, a particular network can be laid out in many completely different ways, most of which tell one very little about its potential correspondence with ordinary space.

So how then can one proceed? The fundamental idea is to look at properties of networks that can both readily be deduced from their pattern of connections and can also be identified, at least in some

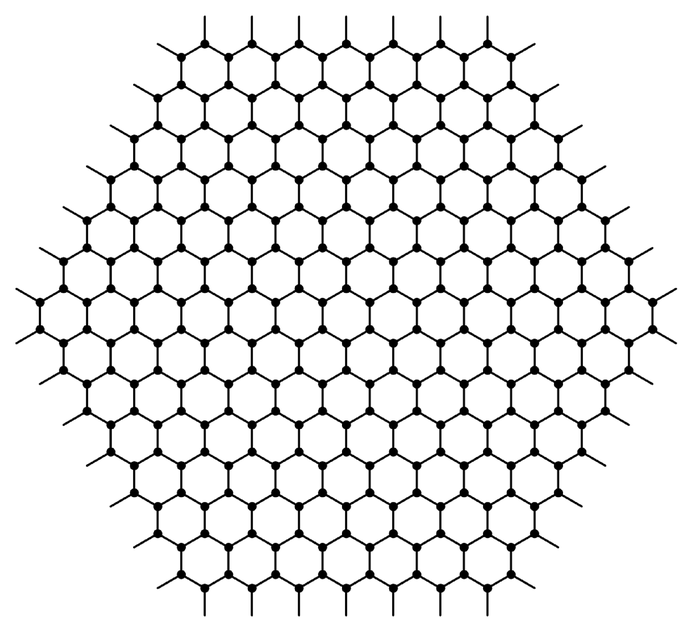Examples of networks with three connections at each node that are effectively one, two and three-dimensional. These networks can be continued forever, and all have the property of being homogeneous, in the sense that every node has an environment identical to every other node.

Six different ways of laying out the same network. (a) nodes arranged around a circle; (b) nodes arranged along a line; (c) nodes arranged across the page according to distance from a particular node; (d) 2D layout with network and spatial distances as close as possible; (e) planar layout; (f) 3D layout.