property that the form of this causal network ends up being the same regardless of the order in which replacements are applied—and thus regardless of the path that is followed in the multiway system.
The pictures below show some simple examples of rules with this property. And as it turns out, it is fairly easy to recognize the presence of the property from the overall pattern of multiway system paths that occur.
If one starts from a given initial string, then typically one will generate different strings by applying different replacements. But if one is going to get the same causal network, then it must always be the case that there are replacements one can apply to the strings one has generated that yield the same final string. So what this means is that any pair of paths in the multiway system that diverge must be able to converge again within just one step—so that all the arrows in pictures like the ones below must lie on the edges of quadrilaterals.
Most multiway systems, however, do not have exactly this property, and as a result the causal networks that are obtained by following different paths in them will not be absolutely identical. But it still turns out that whenever paths can always eventually converge—even if not in a fixed number of steps—there will necessarily be similarities on a sufficiently large scale in the causal networks that are obtained.
At the level of individual events, the structure of the causal networks will typically vary greatly. But if one looks at large enough collections of events, these details will tend to be washed out, and
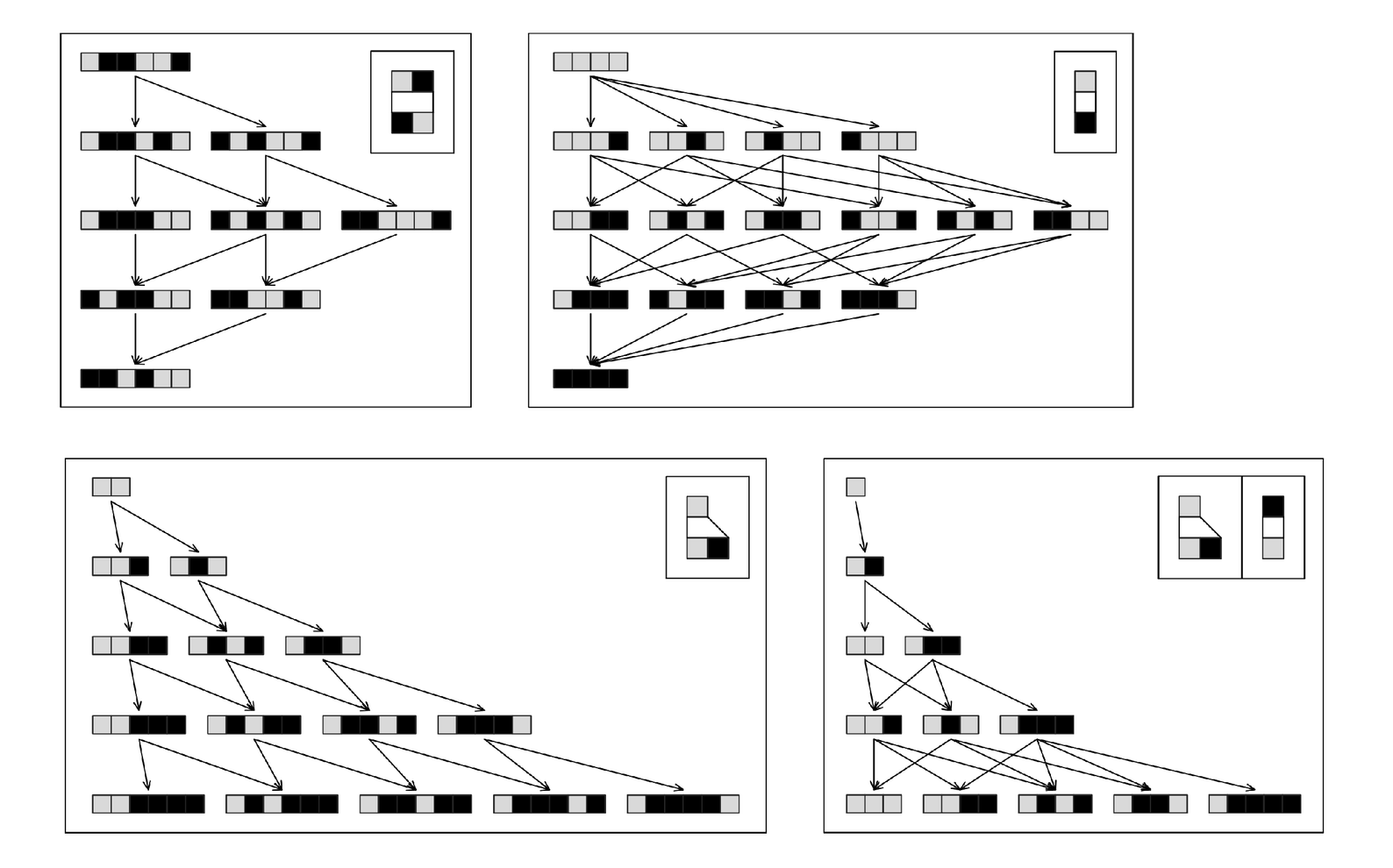
Examples of multiway systems in which the causal network associated with every path is exactly the same. All such multiway systems have the property that every pair of paths which diverge at a particular step can converge again on the following step. The first rule shown has the effect of sorting the elements in the string.



