So what about more general substitution systems? Are there analogs of these for networks? The answer is that there are, and they are based on making replacements not just for individual nodes, but rather for clusters of nodes, as shown in the second set of pictures below.
In the substitution systems for strings discussed in previous sections, the rules that are given can involve replacing any block of elements by any other. But in networks there are inevitably some restrictions. For example, if a cluster of nodes has a certain number of connections to the rest of the network, then it cannot be replaced by a cluster which has a different number of connections. And in addition, one cannot have replacements
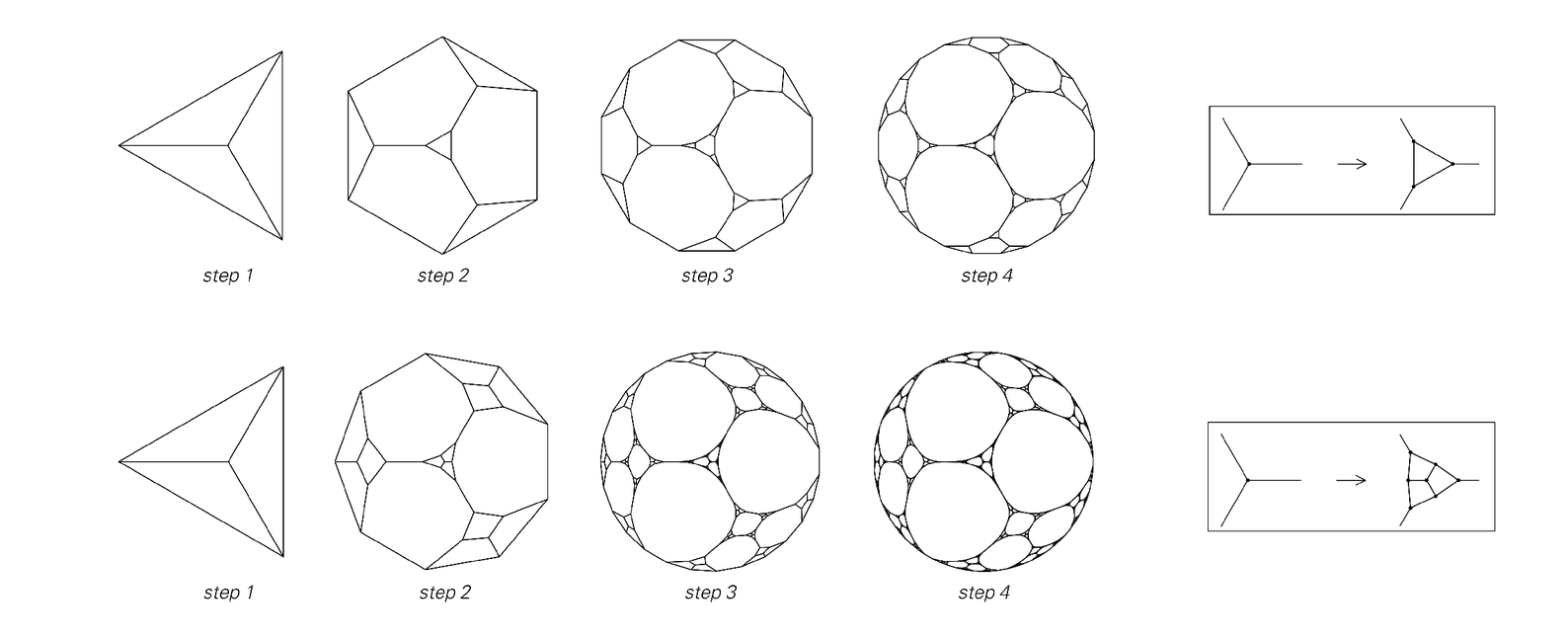
Network evolution in which each node is replaced at each step by a fixed cluster of nodes. The resulting networks have a regular nested form. The dimensions of the limiting networks are respectively Log[2,3] ≃ 1.58 and Log[3, 7] ≃ 1.77.
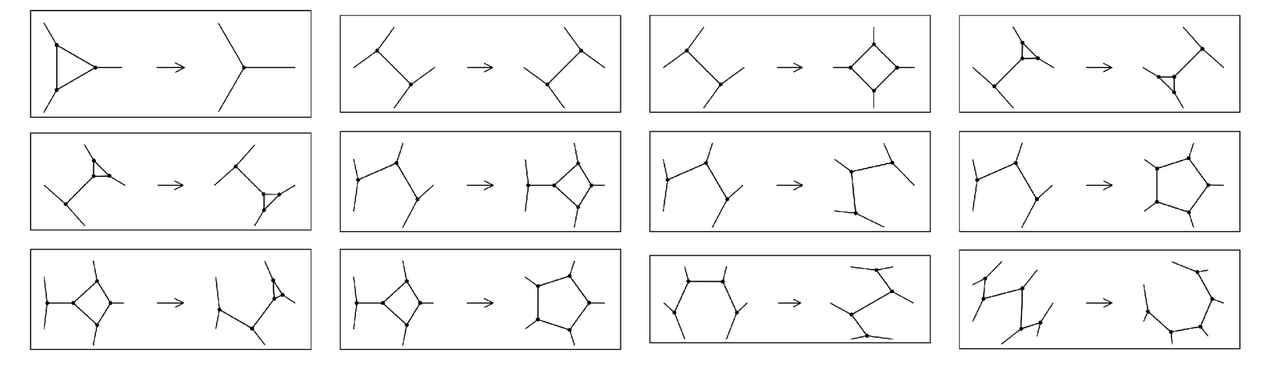
Examples of rules that involve replacing clusters of nodes in a network by other clusters of nodes. All these rules preserve the planarity of a network. Notice that some of them cannot be reversed since their right-hand sides are too symmetrical to determine which orientation of the left-hand side should be used.