like the first picture below that go from a symmetrical cluster to one for which a particular orientation has to be chosen.
But despite these restrictions a fairly large number of replacements are still possible; for example, there are a total of 419 distinct ones that exist involving clusters with no more than five nodes.
So given a replacement for a cluster of a particular form, how should such a replacement actually be applied to a network? At first one might think that one could set up some kind of analog of a cellular automaton and just replace all relevant clusters of nodes at once.
But in general this will not work. For as the second picture below illustrates, a particular form of cluster can in general appear in many overlapping ways within a given network.
The issue is essentially no different from the one that we encountered in previous sections [9, 10, 11] for blocks of elements in substitution systems on strings. But an additional complication is that in networks, unlike strings, there is no immediately obvious ordering of elements.
Nevertheless, it is still possible to devise schemes for deciding where in a network replacements should be carried out. One fairly simple scheme, illustrated on the facing page, allows only a single replacement to be performed at each step, and picks the location of this replacement so as to affect the least recently updated nodes.
In each pair of pictures in the upper part of the page, the top one shows the form of the network before the replacement, and the bottom one shows the result after doing the replacement—with the cluster of nodes involved in the replacement being highlighted in both cases. In the 3D pictures in the lower part of the page, networks that arise on successive steps are shown stacked one on top of the other, with the nodes involved in each replacement joined by gray lines.
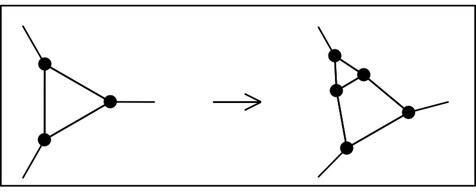
A replacement whose outcome orientation cannot be determined.


The 12 ways in which the cluster of nodes on the bottom left occurs in a particular network. In the particular case shown, each way turns out to overlap with nodes in exactly four others.



