particles in physics one must consider structures on much more complicated and random backgrounds. For any network that has a serious chance of representing actual space—even a supposedly empty part—will no doubt show all sorts of seemingly random activity. So any localized structure that might represent a particle will somehow have to persist even on this kind of random background.

Yet at first one might think that such randomness would inevitably disrupt any kind of definite persistent structure. But the first set of pictures below show two simple examples where it does not. In the first case, there are localized cracks that persist. And in the second case, there are two different types of regions, separated by boundaries that act like localized structures with definite properties, and persist until they annihilate.

So what about networks? It turns out that here again it is possible to get definite structures that persist even in the presence of randomness. And to see an example of this consider setting up rules like those on page 509 that preserve the planarity of networks.

Starting off with a network that is planar—so that it can be drawn flat on a page without any lines crossing—such rules can certainly give all sorts of complex and apparently random behavior. But the way the rules are set up, all the networks they produce must still be planar.

And if one starts off with a network like the one in the bottom picture that can only be drawn with lines crossing, then what will happen is that the non-planarity of the network will be preserved. But to what extent does this non-planarity correspond to a definite structure in the network?

Examples of one-dimensional cellular automata that support various forms of persistent structures even on largely random backgrounds. These are 3-color totalistic rules with codes 294 and 1893.

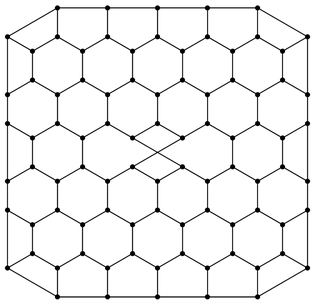
A network with a single irreducible crossing of lines.