In the absence of any gravity or forces, our normal definition of space implies that when an object moves from one point to another, it always goes along a straight line, which corresponds to the shortest path. But when gravity is present, objects in general move on curved paths. Yet these paths can still be the shortest—or so-called geodesics—if one takes space to be curved. And indeed if space has appropriate curvature one can get all sorts of paths, as in the pictures below.
But in our actual universe what determines the curvature of space? The answer from general relativity is that the Einstein equations give conditions for the value of a particular kind of curvature in terms of the energy and momentum of matter that is present. And the point then is that the shortest paths in space with this curvature seem to be
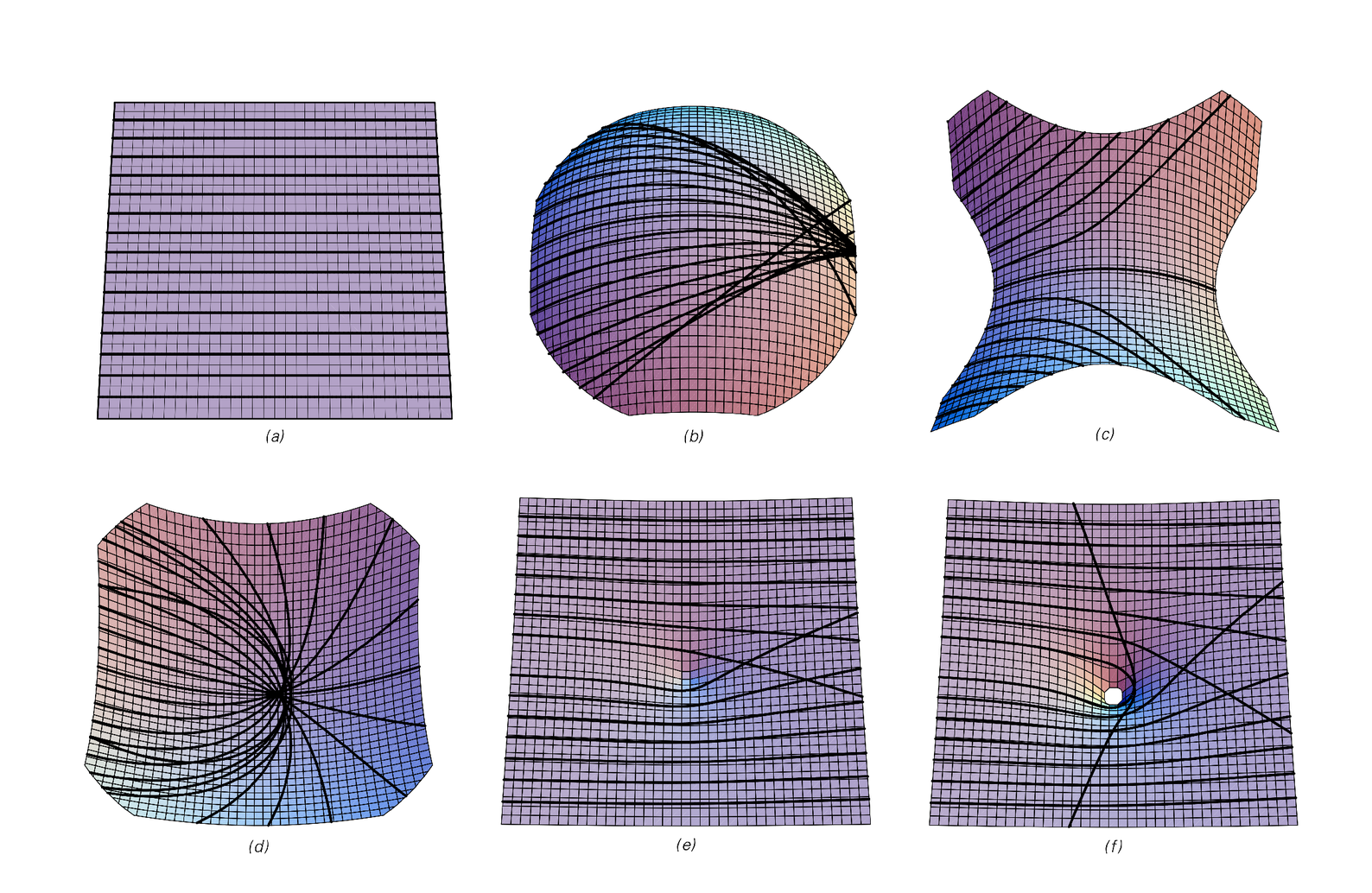
Examples of the effect of curvature in space on paths taken by objects. In each case all the paths shown start parallel, but do not remain so when there is curvature. The paths are geodesics which go the minimum distance on the surface to get to all the points they reach. (In general, the minimum may only be local.) Case (b) shows the top of a sphere, which is a surface of positive curvature. Case (c) shows the negatively curved surface z=x2-y2, (d) a paraboloid z=x2+y2, and (e,f) z=1/(r+δ)—a rough analog of curvature in space produced by a sphere of mass.