The second set of pictures below demonstrates why two-dimensional block encoding does, however, manage to compress it. The point is that the two-dimensional blocks that one forms always contain cells whose colors are connected by the cellular automaton rule—and this greatly reduces the number of different arrangements of colors that can occur.

In cases (e) and (f), however, there is no simple rule for going from one row to the next, and two-dimensional block encoding—like all the other encoding schemes we have discussed so far—does not yield any substantial compression.

Like block encoding, pointer-based encoding can also be extended to two dimensions. The basic idea is just to scan two-dimensional data looking for repeats not of one-dimensional sequences, but instead of two-dimensional regions. And although such a procedure does not in the

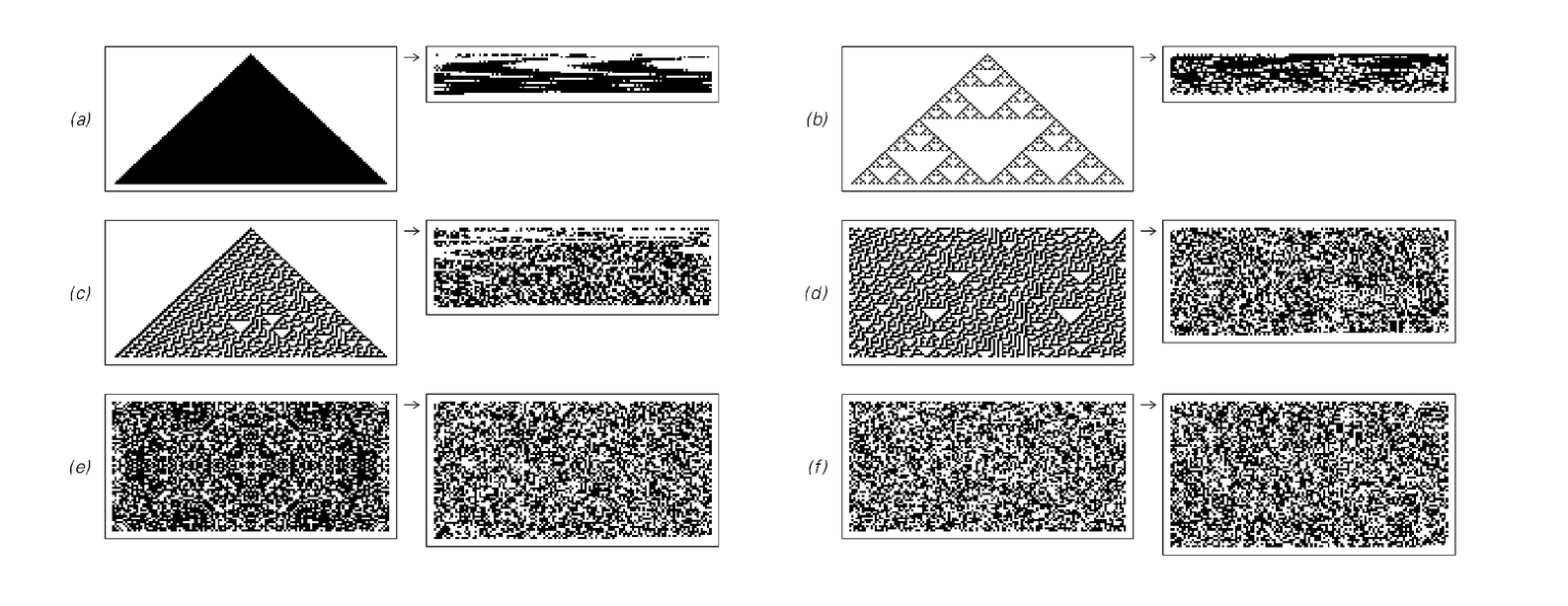
Examples of two-dimensional block-based encoding. Each image is broken into 3×2 blocks, and codewords are then assigned to these blocks using the Huffman scheme. Note the presence of compression even in case (d). This is a consequence of the fact that the cellular automaton rule allows only certain blocks to appear in the pattern, as illustrated in the picture below. (e) is generated by a two-dimensional cellular automaton; (f) is the sequence that appears on the center column of rule 30.

Cellular automaton rule 30, and the 3×2 blocks which appear in large patterns generated by it. There are a total of 2⁶=64 possible 3×2 blocks of black and white cells; the fact that only 24 of them appear in patterns generated by rule 30 is what makes it possible for two-dimensional block-based encoding to compress such patterns.